Thin walled Beams Question
- Thread starter tigerstyle
- Start date
-
- Tags
- Beams
Click For Summary
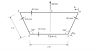
The discussion focuses on calculating the centroid and second moment of area for a hollow thin-walled trapezoidal beam. Participants emphasize the importance of using a systematic approach, including drawing tables to organize areas, distances, and moments for each member. Key formulas mentioned include the centroid formula (c = first moment of area / total area) and the shear flow equation (q = q0 - (Vy/Ixx) ∫ t*y*ds). The conversation also highlights the use of the sine rule for calculating distances in inclined members and the application of the parallel axis theorem for moment of inertia calculations.
PREREQUISITES- Understanding of centroid calculations for geometric shapes
- Familiarity with the second moment of area and its significance in structural analysis
- Knowledge of shear flow concepts and related equations
- Ability to apply the parallel axis theorem in moment of inertia calculations
- Study the derivation and application of the centroid formula in various geometric configurations
- Learn about the calculation of the second moment of area for complex shapes, including inclined surfaces
- Research shear flow analysis in thin-walled structures and its implications on structural integrity
- Explore the parallel axis theorem and its use in transforming moments of inertia for composite sections
Students and professionals in structural engineering, mechanical engineering, and any individuals involved in the analysis and design of thin-walled structures.
Similar threads
- · Replies 8 ·
- · Replies 9 ·
- · Replies 2 ·
- · Replies 45 ·
- · Replies 8 ·
- · Replies 10 ·
- · Replies 1 ·
- · Replies 2 ·
- · Replies 2 ·