Three Pulley - two masses system.

[SciencyBoi]

Homework Statement

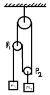
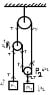
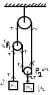
The given system is released from rest. Assuming no friction, mass-less pulleys and ideal strings; calculate the accelerations of the pulleys.

Homework Equations

Constraint equations.
F=ma

The Attempt at a Solution

Taking the above assumptions;

And applying constraints to the longer string, we have;

-a₁ + a₀ + a₀ + 2a₂ - a₀ = 0
=> a₀ + 2a₂ = a₁ ~~~~~~~~~~~~~~~~~~ (1)

Now doing force balancing on m₁;
m₁a₁ = T - m₁g ~~~~~~~~~~~~~~~~~ (2)

similary on m₂;
m₂a₂ = m₂g - 2T ~~~~~~~~~~~~~~~~~~ (3)

For four variables a0, a1, a2 & T; we only have three equations, but we will neeed four. I'm not sure how to get the fourth.

I would greatly appreciate any hint/help.

Thank You...

 

[srecko97]

Consider the relation between a0 and a2 regardful of the highest (the biggest) pulley

 

[srecko97]

Sorry. Never mind! I am not sure any more about my previous comment

 

[ehild]

How is it possible that 2T force acts on pulley P1 downward, and T acts upward? It is a massless pulley.

 

[SciencyBoi]

View attachment 214889How is it possible that 2T force acts on pulley P1 downward, and T acts upward? It is a massless pulley.

I've thought of this;
The upward force is 2T.
Let the downward tension be T'.

Then T' - 2T = 0.a₂
which gives us, 2T = T'

 

[ehild]

I've thought of this;
The upward force is 2T.

Why? It is the same string, the tension is the same everywhere.

 

[srecko97]

It is not the same string

 

[haruspex]

It is not the same string

The roughness of the drawing may be misleading you. It is clearly intended that there is one string from m₁, over P₁, under P₂, over the top pulley and down to the axle of P₁. If not, P₂ is not really a pulley.

 

[srecko97]

Sorry, I know this is the same rope, but I meant the string between p2 and m2. I see that 2T is written next to this string (between p2 and m2) and I see no problem with this.

 

[haruspex]

Sorry, I know this is the same rope, but I meant the string between p2 and m2. I see that 2T is written next to this string (between p2 and m2) and I see no problem with this.

There is no problem with that. Reread post #4. ehild is objecting to the forces shown on P₁.
But of course, it does also appear that those forces shown are correct, since it is all one rope.
What is the resolution to this paradox?

(By the way, to answer the given question it is necessary to assume the pulleys do have some very small mass.)

 

[Abhishek kumar]

There is no problem with that. Reread post #4. ehild is objecting to the forces shown on P₁.
But of course, it does also appear that those forces shown are correct, since it is all one rope.
What is the resolution to this paradox?

(By the way, to answer the given question it is necessary to assume the pulleys do have some very small mass.)

Length of string is constant on the basis of this we can establish relation between acceleration.is there any other method to establish relation between acceleration?

 

[haruspex]

Length of string is constant on the basis of this we can establish relation between acceleration.is there any other method to establish relation between acceleration?

Not sure what you are asking. Are you saying the constant length of string gives one equation, but you do not see how to find a second equation?

 

[Abhishek kumar]

Not sure what you are asking. Are you saying the constant length of string gives one equation, but you do not see how to find a second equation?

No i am saying in constraint motion we can established relation between acceleration. If one displaced say xa other displaced say xb then we establish relation by taking length of string constant. My question is getting same is there amy easier method

 

[haruspex]

No i am saying in constraint motion we can established relation between acceleration. If one displaced say xa other displaced say xb then we establish relation by taking length of string constant. My question is getting same is there amy easier method

No, the constant length of string is a key fact, so you must write an equation expressing that.
Still not sure I understand your question.

 

[SciencyBoi]

I think I got it... When we talk about pulley P2;

Then assuming tension T in the longer string, we would have 2T tension in the string connecting m2 and P2.

However, when we do force balancing of P1;

We would have 2T - T = a₀ x 0;

Which would give us T = 0;

hence the masses m1 and m2 both are effectively in freefall...

Using equation 1(which is derived from the length of string remaining constant) we will have a₀ = 3g.

Thank you everyone... This discussion actually led me to the solution and better concepts...

 

[haruspex]

I think I got it... When we talk about pulley P2;

Then assuming tension T in the longer string, we would have 2T tension in the string connecting m2 and P2.

However, when we do force balancing of P1;

We would have 2T - T = a₀ x 0;

Which would give us T = 0;

hence the masses m1 and m2 both are effectively in freefall...

Using equation 1(which is derived from the length of string remaining constant) we will have a₀ = 3g.

Thank you everyone... This discussion actually led me to the solution and better concepts...

Well done. It was a tricky question.

 

[srecko97]

Yeah, I see that I was really confused. I wanted to help, but I was probably making this task even harder by writing false comments. Please accept my appologies.

 

[SciencyBoi]

Yeah, I see that I was really confused. I wanted to help, but I was probably making this task even harder by writing false comments. Please accept my appologies.

No problem. I honestly appreciate that people took interest in this problem that in no way would benefit them. And I would keep appreciating anyone for their participation in any of the posts here or any of the forums posted by anyone as they intend to help. Intentions is what always matters. Thanks everyone again...