Saladsamurai
- 3,009
- 7
So I was helping my girlfriend with this problem and we are convinced we are correct, but her professor disagrees. So I am taking it to PF court 
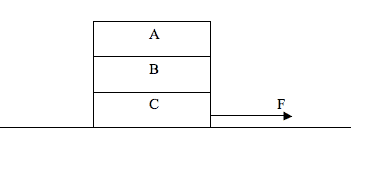
In the figure, all 3 blocks have the same mass. A force pulls the system along the frictionless floor and the 3 blocks all move together in unison.
If the coefficient of static friction between pairs of blocks is the same, compare the magnitudes of net static friction on each block.
Newton's 2nd and the definition of friction: f = mu*Normal
Here is a Free Body Diagram of each block:
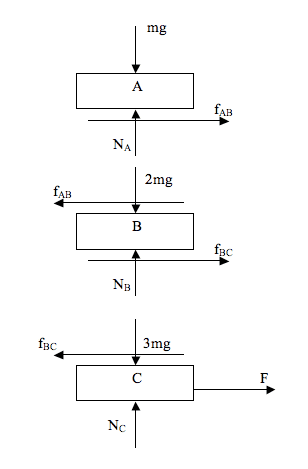
Each pair of blocks has a Newton's 3rd Law reaction pair acting on each face whose magnitude is equal to mu*Normal force.
From Block A
f_{AB}=\mu*N_A = \mu mg
From Block B
f_{BC} = \mu*N_B = 2\mu mg
Therefore the net force from friction on A is given by:
f_{A,Net}=f_{AB} = \mu mg
The net force from friction on B is given by:
f_{B,Net} = f_{BC} - f_{AB} = \mu mg
The net force from friction on C is given by:
f_{C,Net}=f_{BC} = 2\mu mg
Therefore:
f_{A,Net} = f_{B,Net} = \frac{1}{2}f_{C,Net}
I am convinced this is correct, but the answer is supposedly supposed to be:
f_{A,Net} = \frac{1}{2}f_{B,Net} \text{ and } f_{C,Net} = 0
which to me makes no sense. If the NET friction on C was zero, then that would be equivalent to saying there is no friction between blocks C and B which clearly is not true, else block C would accelerate with respect to block B (they would not 'stick' together).
Thoughts from the jury?

Homework Statement
In the figure, all 3 blocks have the same mass. A force pulls the system along the frictionless floor and the 3 blocks all move together in unison.
If the coefficient of static friction between pairs of blocks is the same, compare the magnitudes of net static friction on each block.
Homework Equations
Newton's 2nd and the definition of friction: f = mu*Normal
The Attempt at a Solution
Here is a Free Body Diagram of each block:
Each pair of blocks has a Newton's 3rd Law reaction pair acting on each face whose magnitude is equal to mu*Normal force.
From Block A
f_{AB}=\mu*N_A = \mu mg
From Block B
f_{BC} = \mu*N_B = 2\mu mg
Therefore the net force from friction on A is given by:
f_{A,Net}=f_{AB} = \mu mg
The net force from friction on B is given by:
f_{B,Net} = f_{BC} - f_{AB} = \mu mg
The net force from friction on C is given by:
f_{C,Net}=f_{BC} = 2\mu mg
Therefore:
f_{A,Net} = f_{B,Net} = \frac{1}{2}f_{C,Net}
I am convinced this is correct, but the answer is supposedly supposed to be:
f_{A,Net} = \frac{1}{2}f_{B,Net} \text{ and } f_{C,Net} = 0
which to me makes no sense. If the NET friction on C was zero, then that would be equivalent to saying there is no friction between blocks C and B which clearly is not true, else block C would accelerate with respect to block B (they would not 'stick' together).
Thoughts from the jury?