Tj's question at Yahoo Answers regarding finding the area between two functions

[MarkFL]

Here is the question:

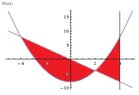
Find the area between the curves?

Find the area between the curves y= x^2 -8, y= -2x, and x=4

The teacher says the integral setup is
Area= Integral:(-4 to 2) (-2x- x^2 +8)dx + Integral:(2 to 4) (x^2 -8 + 2x) dx

How did the teacher get that?

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Re: Tj's question at Yahoo! Anwwers regarding finding the area between two functions

Hello Tj,

The area between two curves is given by:

\(\displaystyle A=\int_a^b\left|f(x)-g(x) \right|\,dx\)

In order to get rid of the absolute value, we need to make sure we have a non-negative integrand, that is we have the greater function minus the lesser function. Let's take a look at the area in question for this problem:

View attachment 1098

We see that the linear function is greater than the quadratic in between their points of intersection, and then the quadratic is the greater function to the right of the points of intersection, but to the left of the bounding line $x=4$.

So, we need to determine the $x$-coordinates of the intersection points, so we may equate the two function and solve for $x$:

\(\displaystyle x^2-8=-2x\)

\(\displaystyle x^2+2x-8=0\)

\(\displaystyle (x+4)(x-2)=0\)

Hence, we find \(\displaystyle x=-4,2\).

So, we find that given area with:

\(\displaystyle A=\int_{-4}^2(-2x)-\left(x^2-8 \right)\,dx+\int_2^4 \left(x^2-8 \right)-(-2x)\,dx\)

Simplify:

\(\displaystyle A=\int_{-4}^2 8-2x-x^2\,dx+\int_2^4 x^2+2x-8\,dx\)

This is equivalent to what your teacher gave. Let's go ahead and find the area:

\(\displaystyle A=\left[8x-x^2-\frac{1}{3}x^3 \right]_{-4}^2+\left[\frac{1}{3}x^3+x^2-8x \right]_2^4=\)

\(\displaystyle \left(8(2)-(2)^2-\frac{1}{3}(2)^3 \right)-\left(8(-4)-(-4)^2-\frac{1}{3}(-4)^3 \right)+\left(\frac{1}{3}(4)^3+(4)^2-8(4) \right)-\left(\frac{1}{3}(2)^3+(2)^2-8(2) \right)=\)

\(\displaystyle \frac{28}{3}+\frac{80}{3}+\frac{16}{3}+\frac{28}{3}=\frac{152}{3}\)