To calculate torque on a supported beam

[gnits]

Homework Statement

To calculate torque on a supported beam

Relevant Equations

equate forces and torques

Could I please ask for help with the last part of the following question?

I have the first two parts done, answers are:

Distance of COG from A = a(1+n)/n

and W1 = W(1+n)/3

I can't see how to go about the last part. Here's my diagram for the system prior to the torque L being added:

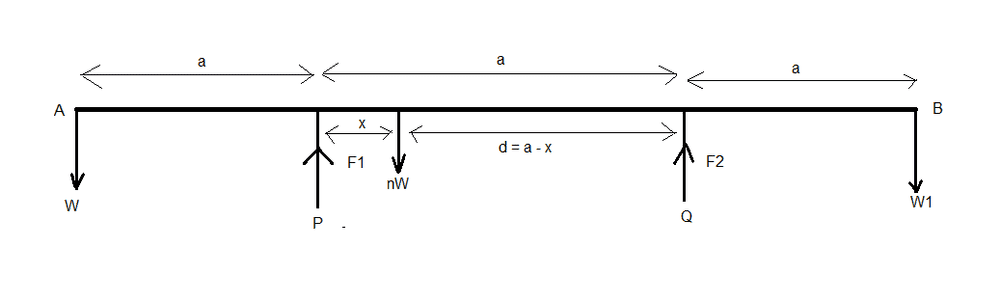
In this situation we have (are told) F1 = F2 = F say, and so W1 + W + nW = 2F and so as we know W1 in terms of W and n we have F = 2W(n+1)/3 and we are told that after torque L is applied then this increases by 1.5 times, so now F1 = W(n+1) and so F2 = W(n+1)/3. As F1 has increased then we know that L is counter-clockwise.

Can't see though what equation to set up to calculate the L which would lead to this value for F1.

Thanks for any help,
Mitch.

 

[haruspex]

Of all the forces acting on the beam after L is applied, which is the one that you neither know nor care about? What axis can you take moments about to avoid involving that force?

 

[gnits]

Of all the forces acting on the beam after L is applied, which is the one that you neither know nor care about? What axis can you take moments about to avoid involving that force?

Thanks very much. That helped me to see it. Moments about Q.

Mitch.