gnits
- 137
- 46
- Homework Statement
- To find forces in a framework
- Relevant Equations
- Equating of forces
Moments
A very simple (I thought!) question:
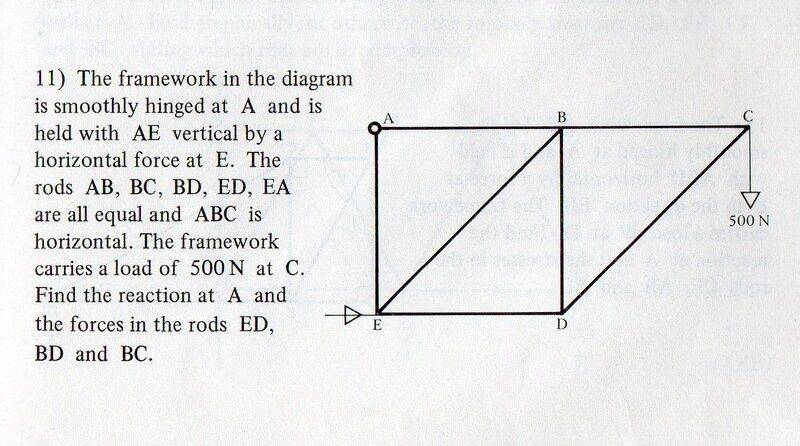
I'm just looking at the first part, finding the reaction at the hinge A.
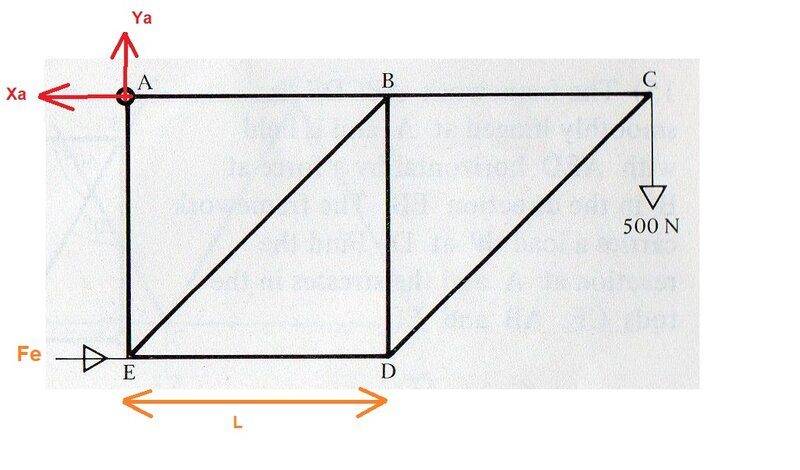
Here is my annotated diagram, with the reaction and A resolved into it's X and Y components, the force at E labelled as Fe and the length of ED labelled as L.
Considering the body as a whole:
Resolving vertically:
Ya = 500
Taking moments about E:
Xa * L = 2 * L * 500
which gives Xa = 1000
So the resultant at A will have size sqrt(1000^2 + 500^2) = 1118 (approx.)
Answer given in book is 112 N at 26.6⁰ below the horizontal.
My answer is very different and also above the horizontal.
What simple mistake have I made in my reasoning?
Thanks.
I'm just looking at the first part, finding the reaction at the hinge A.
Here is my annotated diagram, with the reaction and A resolved into it's X and Y components, the force at E labelled as Fe and the length of ED labelled as L.
Considering the body as a whole:
Resolving vertically:
Ya = 500
Taking moments about E:
Xa * L = 2 * L * 500
which gives Xa = 1000
So the resultant at A will have size sqrt(1000^2 + 500^2) = 1118 (approx.)
Answer given in book is 112 N at 26.6⁰ below the horizontal.
My answer is very different and also above the horizontal.
What simple mistake have I made in my reasoning?
Thanks.