Help Solving 2 Qs: Tan(Ɵ) & Sign Direction Error

[gnits]

Homework Statement

To find possible angle of two leaning rods

Relevant Equations

moments

Could I please ask for help with the following question:

The last part follows easily from the first part.

Answer from back of book for first part is:

2/(3u') <= tan(Ɵ) <= 2u

What I have done is the following:

Here's my diagram (I have separated the components to show the internal forces in the system. I have used t instead of Ɵ) :

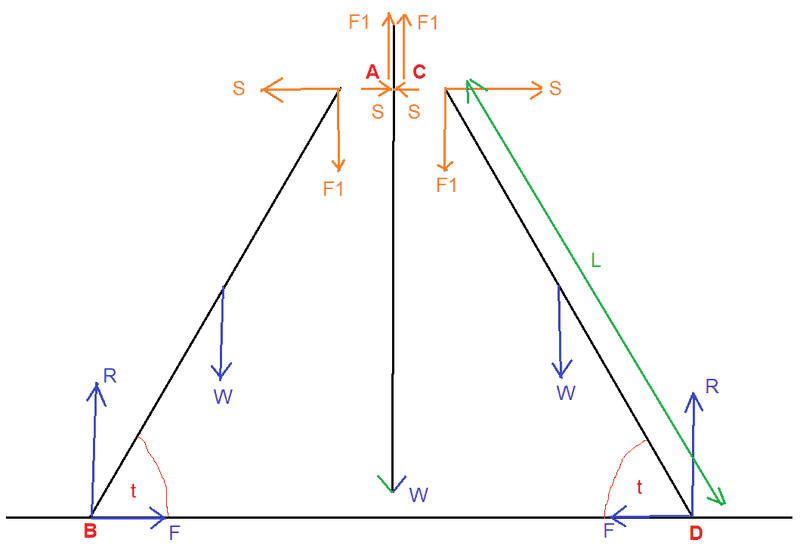
Orange forces are internal forces.

If I equate forces for the whole system vertically I get:

R = (3/2)W

If I equate forces vertically for the vertical rod only I get:

F1 = W/2

If I take clockwise moments about C for rod CD only I get:

F * L sin(t) + W * (L/2) cos(t) = R * L cos(t)

Substituting for R and rearranging gives: F = W / tan(t)

Now for no slipping at D we need F <= u' R so this gives:

W/tan(t) <= u' * (3/2)W

Which leads to tan(t) <= 2/(3u') which is the answer asked for but with the sign reversed.

1) How have I gotten the sign mixed up?

Taking clockwise moments about D for rod CD only I get:

S * L sin(t) = F1 * L cos(t) + W * (L/2) * cos*(t)

Substituting for F1and rearranging gives:

S = W/tan(t) and for no slipping at C we need S <= u * F1

So gives W/tan(t) <= u * W/2 which leads to tan(t) >= 2/u

Again wrong direction of sign and also wrong answer as we need tan(t) <= 2u

2) Where have a erred?

Thanks for any help.

 

[gnits]

Thank you very much kuruman for your reply.

So, notwithstanding the signs, would you (or others) think my analysis of taking moments for CD only about D looks correct? I ask because here I differ in the actual form of the answer. The given answer is 2u but I arrive at 2/u. If you\others agree that 2/u is correct then I would put it down to a typo in the book.

Thanks again.

 

[PeroK]

Now for no slipping at D we need F <= u' R so this gives:

W/tan(t) <= u' * (3/2)W

Which leads to tan(t) <= 2/(3u') which is the answer asked for but with the sign reversed.

I agree with the first equation here, but that implies that $\mu' \tan \theta \ge \dfrac 2 3$.

 

[gnits]

I agree with the first equation here, but that implies that $\mu' \tan \theta \ge \dfrac 2 3$.

Yes indeed, I agree. I had fallen at the last there. Thanks for that. So only the second part is now causing me issues.

 

[PeroK]

S = W/tan(t) and for no slipping at C we need S <= u * F1

For no slipping we need $\mu S \ge F_1 = \dfrac{mg}{2}$.

$S$ is the normal force and $F_1$ is the required friction force.

 

[gnits]

For no slipping we need $\mu S \ge F_1 = \dfrac{mg}{2}$.

$S$ is the normal force and $F_1$ is the required friction force.

Thanks very much indeed. I had swapped S and F1. I had written S <= u * F1 whereas, as you say, I should have written F1 <= u S. And indeed this leads to the book's answer. Thank you very much.

 

[kuruman]

Thank you very much kuruman for your reply.

So, notwithstanding the signs, would you (or others) think my analysis of taking moments for CD only about D looks correct? I ask because here I differ in the actual form of the answer. The given answer is 2u but I arrive at 2/u. If you\others agree that 2/u is correct then I would put it down to a typo in the book.

Thanks again.

Sorry, I deleted my reply to write a better one, but then I had an emergency that kept me away from the task. You must have read my post soon after I posted it but before I deleted it. Anyway, it looks like your issue has been resolved so there is nothing more for me to say. I apologize for the confusion.