gnits
- 137
- 46
- Homework Statement
- To find the time to nearest appoach of a dinghy and a buoy
- Relevant Equations
- d=st
Can anyone please help me see if my reasoning is correct regarding the following question?
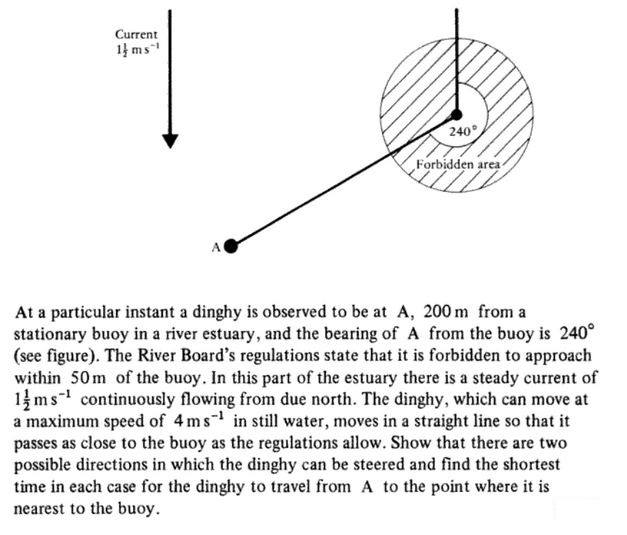
I'll just solve for the case where the dinghy tracks so as to just 'touch' the exclusion zone on the 'high' side
So, in the diagram below:
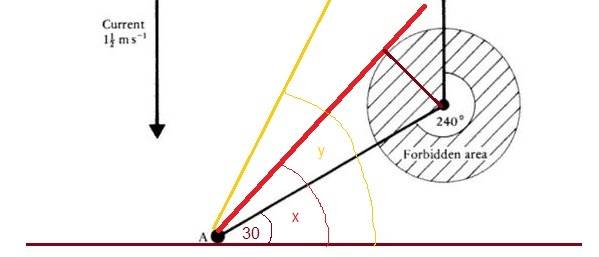
The dinghy tracks along the red path, inclined at x degrees to 'east'. In order to achieve this in the face of the current it will have to point in the direction of the orange line, inclined at y degress to 'east'
In the triangle we know the length of the black side is 200 and so we can calculate the length of the red side (from A to point of closest approach) as the triangle is a right triangle, this gives the red side of the trianlge a length of 50√17 and the angle in the triangle at A works out at atan(1/4) = 14.04 degrees.
Therefore x = 30 + 14.04 = 44.04
So from this we can say that if the boat were to set off along the orange line at full speed then it would be pushed back along the red line by the current, this would give: (let i and j be unit vectors in the direction east and north respectively and V the veclocity of the dinghy along the red track)
4 cos(y) i + 4 sin(y) j - (3/2) j = V cos (44.04) i + V sin (44.04) j
Equating i and j components gives:
4 cos(y) = V cos (44.04)
and
4 sin(y) - (3/2) = V sin(44.04)
So now I can eliminate cos(y) and sin(y) using sin^2 + cos^2 = 1 to solve for V, which comes out as V = 3.6226 and so the time required is 50√17/3.6226 = 57 seconds.
I can repeat this for the 'lower' side of the exclusion zone and it's all the same except that now x = 30 - 14.04 = 15.96 and this leads to V = 4.1 and so t = 50√17/4.1 = 50 seconds.
(The answers given in the book are 69 and 58 seconds)
Thanks for any help,
Mitch.
I'll just solve for the case where the dinghy tracks so as to just 'touch' the exclusion zone on the 'high' side
So, in the diagram below:
The dinghy tracks along the red path, inclined at x degrees to 'east'. In order to achieve this in the face of the current it will have to point in the direction of the orange line, inclined at y degress to 'east'
In the triangle we know the length of the black side is 200 and so we can calculate the length of the red side (from A to point of closest approach) as the triangle is a right triangle, this gives the red side of the trianlge a length of 50√17 and the angle in the triangle at A works out at atan(1/4) = 14.04 degrees.
Therefore x = 30 + 14.04 = 44.04
So from this we can say that if the boat were to set off along the orange line at full speed then it would be pushed back along the red line by the current, this would give: (let i and j be unit vectors in the direction east and north respectively and V the veclocity of the dinghy along the red track)
4 cos(y) i + 4 sin(y) j - (3/2) j = V cos (44.04) i + V sin (44.04) j
Equating i and j components gives:
4 cos(y) = V cos (44.04)
and
4 sin(y) - (3/2) = V sin(44.04)
So now I can eliminate cos(y) and sin(y) using sin^2 + cos^2 = 1 to solve for V, which comes out as V = 3.6226 and so the time required is 50√17/3.6226 = 57 seconds.
I can repeat this for the 'lower' side of the exclusion zone and it's all the same except that now x = 30 - 14.04 = 15.96 and this leads to V = 4.1 and so t = 50√17/4.1 = 50 seconds.
(The answers given in the book are 69 and 58 seconds)
Thanks for any help,
Mitch.
Last edited: