unknown1111
- 7
- 3
Does it make sense to talk about the top mass at energies below mt, although in all processes the corresponding energy scale is above mt because of the rest mass energy of the top quark?
Using an effective field theory approach, the top quark decouples at energies below the top quark mass and therefore has no influence on the mass running of the other fermions. Nevertheless, it is possible to compute how the top quark mass mt changes at energies below mt, for example, because of the energy dependence of the gauge coupling constants. For example, in Updated Estimate of Running Quark Masses the authors compute
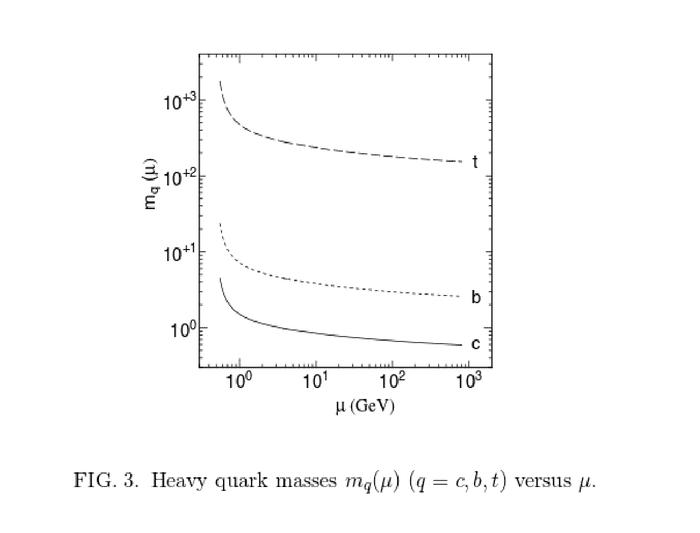
Imagine, for example, the top would be stable for some reason and we could determine its mass somehow using a "scale" at low energies. Would we get the top mass at "room temperature", i.e. a few milli-GeV or only always its mass at around 200 GeV, because of the rest mass energy of the top quark?
Using an effective field theory approach, the top quark decouples at energies below the top quark mass and therefore has no influence on the mass running of the other fermions. Nevertheless, it is possible to compute how the top quark mass mt changes at energies below mt, for example, because of the energy dependence of the gauge coupling constants. For example, in Updated Estimate of Running Quark Masses the authors compute
Imagine, for example, the top would be stable for some reason and we could determine its mass somehow using a "scale" at low energies. Would we get the top mass at "room temperature", i.e. a few milli-GeV or only always its mass at around 200 GeV, because of the rest mass energy of the top quark?