Physical_Fire
- 54
- 11
- Homework Statement
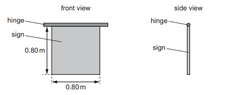
- A uniform square sign of weight 40 N is suspended vertically from its top edge by a horizontal hinge, as shown. The hinge is not frictionless. When the sign is displaced from the vertical by an external force and then released, it does not return to the vertical position. The maximum torque exerted by the hinge on the sign is 6.0 N m. The sign is displaced by 90 degrees so that it is horizontal and then gradually released. At which angle to the vertical does the sign hang after release? Write out your thought process and understanding as well. (5)
- Relevant Equations
- T= F*D
Since I understood that torque = net moment, and as it said angle from the vertical, I used the equation t = F*d*cosx. So, 6 = 40*0.4*cosx, x = 68 degrees. I got a zero out of 5 in this question because the thought process was wrong as well as the answer. I do not understand this problem beyond the equations involved. Why is the answer wrong and what is the real concept and understanding behind these problems?
Thanks
Thanks
Attachments
Last edited: