Torques exerted on a vertical disk by multiple forces

[paulimerci]

Homework Statement

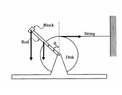
A uniform disk is mounted to an axle and is free to rotate without friction. A thin uniform rod is rigidly attached to the disk. A block is attached to the end of the rod. Properties of the rod, and block are as follows.
Rod: mass=m, length = 2R
Block: mass= 2m
Disk: radius =R The system is held in equilibrium with the rod at an angle theta 0 to the vertical, as shown in the figure, by a horizontal string of negligible mass with one end attached to the disk and the other to a wall. Determine the tension in the string in terms of m, theta 0, and g.

Relevant Equations

T = Fx R x sin ϴ

This was how the solution was arrived in the text,
Net torque = F block x d block x sin ϴ0 + F rod x d rod x sin ϴ0 - T R sin 90
0 = 2mg x 2R x sin ϴ0 + m x R x sinϴ0 - T R
T = 5 mg sinϴ0
I'm wondering do we have to resolve the forces for rod and block in to components here and find for the component which is perpendicular to the vertical. I'm confused could anyone help me.

 

[Lnewqban]

As the probem gives you R, yes, you are forced to determine the vertical component of weight.

 

[paulimerci]

As the probem gives you R, yes, you are forced to determine the vertical component of weight.

As the probem gives you R, yes, you are forced to determine the vertical component of weight.

Is the vertical component sin theta here, can anyone explain how?

 

[paulimerci]

I mean is the perpendicular component here is sin theta?

 

[haruspex]

do we have to resolve the forces for rod and block in to components here and find for the component which is perpendicular to the vertical.

The formula is force x (distance from axis to point of application) x (sine of angle between).
Equivalently, either
force x (perpendicular distance from axis to line of application), or
(component of force perpendicular to distance from axis to point of application) x (distance from axis to point of application).
So in the present case you can either find the horizontal distances from axis to forces or find the components of the forces normal to the rod.

 

[kuruman]

Please study the diagram below. There is a position vector $\mathbf{r}$ and force vector $\mathbf{F}.$ Then there is component $r_{\perp}$ perpendicular to the line of action of $\mathbf{F}$ and component $F_{\perp}$ perpendicular to the direction of $\mathbf{r}.$ The magnitude of the torque is
$$\tau=rF_{\perp}=r_{\perp}F=rF\sin\theta.$$There is nothing more to it. Draw the dotted lines either along the forces or along the positions and figure it out.