Discussion Overview
The discussion revolves around the dynamics of a uniform rod being pushed horizontally while maintaining a vertical orientation. Participants explore the forces and torques involved, particularly focusing on the role of a counterweight to prevent rotation due to an off-axis thrust applied below the center of mass. The conversation includes calculations for required counterweight mass under different acceleration scenarios.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
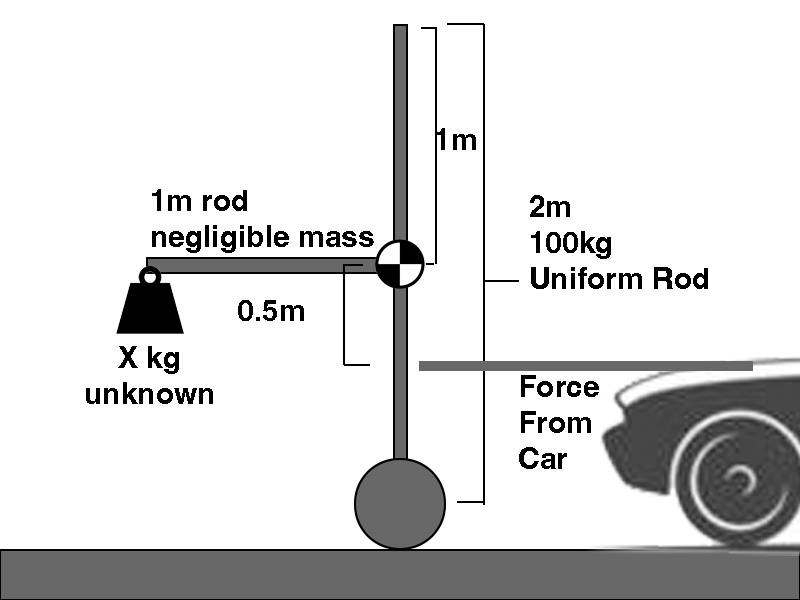
- One participant describes a scenario involving a 2m, 100kg rod with wheels, pushed horizontally 0.5m below its center of mass, and seeks to calculate the mass of a counterweight needed for specific accelerations.
- Another participant questions the mass of the wheels, suggesting it could affect the center of mass of the rod.
- Some participants propose that the push force from the car causes a clockwise torque, necessitating a counter torque from the counterweight to maintain verticality.
- Calculations are presented for counterweight mass based on different push forces, with specific values leading to total mass and acceleration results.
- Several participants emphasize the importance of posting Free Body Diagrams (FBD) to clarify forces and torques acting on the system.
- There is confusion expressed regarding how to target a specific acceleration when the mass including the counterweight is dependent on the force applied.
- One participant notes that if the counterweight is too light, it could lead to tipping over when the car is not pushing the rod forward.
Areas of Agreement / Disagreement
Participants generally agree on the need for a counterweight to prevent rotation, but there is no consensus on the specific calculations or the implications of the forces involved. The discussion remains unresolved regarding the best approach to determine the necessary counterweight mass and the dynamics of the system.
Contextual Notes
Participants highlight the complexity of the problem, noting that the arrangement may lead to different behaviors under varying conditions, such as the mass of the wheels and the fixed torque-arm lengths. There are also concerns about the assumptions made regarding the system's motion and the effects of the counterweight.
Who May Find This Useful
This discussion may be useful for individuals interested in dynamics, mechanical engineering, and physics, particularly those exploring torque, force diagrams, and the balance of forces in systems involving rotational motion.