B Torsion Involving an Off Axis Thrust

[jrmichler]

Still no FBD after 30 posts, so time to fix that. The vertical rod weighs 100 kg, and the wheels at the bottom have zero mass, so that rod is shown as a 100 kg mass at the rod center of mass (COM), which is 1 m above the ground. A mass M is at the same height as the COM of the rod, and 1 m to the left of the rod COM. The assembly is vertically supported by a vertical force at the bottom of the rod; that force is $(100 + M) * 9.8$ N. There is no horizontal force at the bottom of the rod because these are physics wheels - zero mass, zero friction.

The total mass is 100 + M, and the acceleration, $a$, is unknown, so the total acceleration force is $(100 + M) * a$. There is an equal and opposite force $(100 + M) * a$ from the car applied at point P. The FBD shows this:

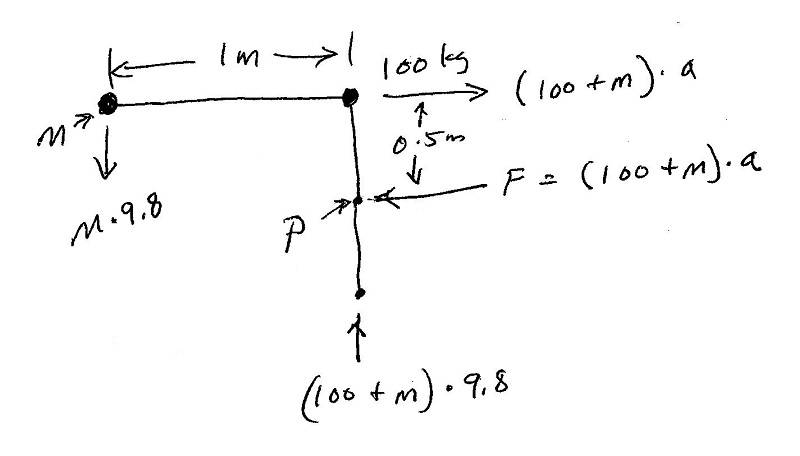
Everything is in equilibrium. The total vertical force down is $(100 + M) * 9.8$ N, which is balanced by the vertical force up at the wheels. The total horizontal force due to the acceleration is balanced by the force from the car. The only unknown is the acceleration, which is calculated by taking a sum of moments about a convenient point. The two most convenient points are the COM of the 100 kg rod, and the point P where the force from the car is applied. Arbitrarily choosing to take moments about point P, the calculation is as follows:

The mass M has a moment $M * 9.8 m/s^2 * 1 m = 9.8M$ Nm. The acceleration force has a moment $(100 + M) * a * 0.5m = 0.5 * a * (100 + M)$ Nm in the opposite direction. So the final equation for a is $$9.8M - 0.5 * a * (100 + M) = 0$$
One equation with one unknown, solve for a. Alternatively, you can define the acceleration with the mass M unknown, and solve for M.

 

[Baluncore]

To make the model easy to compute:
1. Keep it vertical and rotation free, by balancing the torques.
2. Specify the mass of counterweight, C. Let it slide along and clamp to a rod, at position L1.
3. The mass of that rod can be balanced by the mass of the car push rod.
4. The car pushes on a point L2 below the CofM.
5. That keeps the CofM above the wheel.

 

[Devin-M]

Correct me if I’m wrong, but in this drawing the counterweight M is unnecessary because the force from the car is being applied directly through the center of mass of the 100kg rod. The problem I wanted to solve for is when the force is applied 0.5m beneath the center of mass of the 100kg, 2m long rod (before counterweight added). The counterweight’s purpose is to counter the backwards tilting torque caused by the force being applied below the center of mass.

 

[DaveC426913]

If we attach a bracket of negligible mass as shown, we can eliminate angle D and L2 from the previous force diagram, but we still need to determine L1:

View attachment 330239

The addition of that bracket has exactly zero effect on the problem or solution.

 

[Devin-M]

I will attempt to solve this with a 5kg counterweight.

We have:
Counterweight: 5kg
Rod: 100kg

Center of Mass Equation

((5*0)+(100*1))/(5+100) = 0.9523m

^Center of mass is 0.95m from Counterweight

Torque from counterweight:

5kg*9.8m/s^2*0.95m = 46.55Nm torque from counterweight

Force from car:

46.55Nm / 0.5m = 93.1 N force from car

Acceleration from force & mass:

93.1N / (100kg + 5kg) = 0.88m/s^2 acceleration

 

[jrmichler]

Correct me if I’m wrong

Look carefully at the dimensions in the FBD. The portion of the vertical rod that is above the COM is not shown because it has no mass, and therefore no effect on the solution. The wheels are massless, so the FBD has exactly two masses, both of which are shown as point masses:
1) The COM of the vertical rod.
and
2) The added mass out in front.

Since this problem is defined as translation only, with zero rotation, all masses are shown at their COM. If you were working on a different problem involving angular acceleration, you would need to show distributed masses as distributed masses. The vertical rod would be one such mass.

The secret to solving these types of problems is to put most of your effort into getting the FBD correct, and without any extraneous detail. The best FBD has only the information needed to solve the problem.

If you want to better understand FBD's, solve this one several different ways:
1) By sum of moments about point P, the point of application of the force from the car.
and
2) By sum of moments about the COM of the vertical rod.
and
3) By sum of moments about the mass M.
and
4) By sum of moments about the center of the wheels.

According to this page,

Looking for an equation online will, all too often, lead you to a wrong answer because there is no guarantee that the online equation is correct for your FBD. If the FBD is correct, then the correct equation is easily found.

 

[Devin-M]

The portion of the vertical rod that is above the COM is not shown because it has no mass, and therefore no effect on the solution.

That portion weighs 50kg-- the 2m uniform rod is 100kg, so the half above that point is 50kg.

 

[Devin-M]

Only the horizontal rod has negligible mass.

 

[jrmichler]

OOPS, my bad. Good catch. But, because this problem is translation only, the vertical rod is shown as a 100 kg point mass.

 

[Devin-M]

OOPS, my bad. Good catch. But, because this problem is translation only, the vertical rod is shown as a 100 kg point mass.

The rod in the problem is not a point mass, so depending where the force is applied (below or above the center of mass), there is either a backwards tilting or forwards tilting torque from the thrust from the car (in this case a backwards tilting torque from the thrust from the car, because the thrust is applied 0.5m below the center of mass of the vertical rod).

 

[berkeman]

The rod in the problem is not a point mass, so depending where the force is applied (below or above the center of mass), there is either a backwards tilting or forwards tilting torque from the thrust from the car (in this case a backwards tilting torque from the thrust from the car, because the thrust is applied 0.5m below the center of mass of the vertical rod).

I haven't been following your thread lately, but my impression all along was that you want to do the calculation for the situation where the vertical rod does not rotate, right? So there are no MOI considerations...

 

[Devin-M]

I haven't been following your thread lately, but my impression all along was that you want to do the calculation for the situation where the vertical rod does not rotate, right? So there are no MOI considerations...

The problem is that without the counterweight, the main rod would tend to tilt backwards (top towards car) as it is accelerated from the thrust from the car below the rod's center of mass (horizontal thrust applied below center of mass of main 100kg uniform rod). The counterweight is added to counter this torque resulting in net 0 torque composed of 2 equal torques in opposite directions, and an acceleration from the force from the car in the horizontal direction.

 

[Baluncore]

I keep thinking that it will all end in a tangled mess. As the car accelerates steadily things are OK, but when the car becomes torque limited at high RPM, the counterweight will fall forwards, and the car will run over the contraption, hence, the tangled mess.

 

[Devin-M]

I believe I was able to solve counterweight mass KG for a desired acceleration...

A = Acceleration m/s^2 = 1
B = Counterweight Mass kg =
C = Car Force Distance From COM meters = 0.5
D = Main Rod Mass kg = 100
G = Acceleration of Gravity m/s^2 = 9.8

B = (D*C^2*A+D^2*C*A)/(D*G-C^2*A-D*C*A)

B = (100*0.5^2*1+100^2*0.5*1)/(100*9.8-0.5^2*1-100*0.5*1)

5.4kg = (100*0.5^2*1+100^2*0.5*1)/(100*9.8-0.5^2*1-100*0.5*1)

^5.4kg counterweight mass is needed for 1m/s^2 acceleration

 

[Baluncore]

What happens when you set the required acceleration to 10.0 ?

 

[Devin-M]

Please disregard the previous formula I posted-- it's in error.

I went back to specifying the counterweight mass (without knowing acceleration) and discovered there is a certain point when you keep increasing the counterweight mass the acceleration starts going back down... for example 300kg counterweight has lower acceleration than 100kg counterweight.

 

[Devin-M]

90kg Counterweight:
Center of Mass
((90*0)+(100*1))/(90+100) = 0.5263m
^Center of mass is 0.5263m from Counterweight
Torque from counterweight:
90kg*9.8m/s^2*0.5263m = 464.19Nm torque from counterweight
Force from car:
464.19Nm / 0.5m = 928.38 N force from car
Acceleration from force & mass:
928.38N / (90kg + 100kg) = 4.8862m/s^2 acceleration

100kg Counterweight:
Center of Mass
((100*0)+(100*1))/(100+100) = 0.5m
^Center of mass is 0.5m from Counterweight
Torque from counterweight:
100kg*9.8m/s^2*0.5m = 490Nm torque from counterweight
Force from car:
490Nm / 0.5m = 980 N force from car
Acceleration from force & mass:
980N / (100kg + 100kg) = 4.9m/s^2 acceleration

110kg Counterweight:
Center of Mass
((110*0)+(100*1))/(110+100) = 0.476m
^Center of mass is 0.476m from Counterweight
Torque from counterweight:
110kg*9.8m/s^2*0.476m = 513.128Nm torque from counterweight
Force from car:
513.128Nm / 0.5m = 1026.25 N force from car
Acceleration from force & mass:
1026.25N / (110kg + 100kg) = 4.88m/s^2 acceleration

300kg Counterweight:
Center of Mass
((300*0)+(100*1))/(300+100) = 0.25m
^Center of mass is 0.25m from Counterweight
Torque from counterweight:
300kg*9.8m/s^2*0.25m = 735Nm torque from counterweight
Force from car:
735Nm / 0.5m = 1470 N force from car
Acceleration from force & mass:
1470N / (300kg + 100kg) = 3.67m/s^2 acceleration

 

[Devin-M]

It looks like acceleration peaks at 1/2 of Earth's gravitational acceleration, when the counterweight mass equals the main rod mass, then acceleration decreases with additional counterweight mass... which implies you can't calculate the counterweight mass from the desired acceleration because there's more than 1 solution, and the peak horizontal acceleration is 1/2 of Earth's 9.8m/s^2 vertical gravitational acceleration.

 

[Devin-M]

If there were no counterweight and stable acceleration were achieved by setting an initial forward lean angle, would there be any further acceleration to be gained by using a counterweight in addition to the forward lean angle?

 

[Devin-M]

If there were no counterweight and stable acceleration were achieved by setting an initial forward lean angle, would there be any further acceleration to be gained by using a counterweight in addition to the forward lean angle?

The reason I ask is some electric skateboard riders showed me they are getting around 1g acceleration from leaning alone…

 

[jbriggs444]

The reason I ask is some electric skateboard riders showed me they are getting around 1g acceleration from leaning alone…

You can get arbitrarily high acceleration by leaning alone. Take the arc tangent of the horizontal acceleration in g's. The acceleration in g's is also the required coefficient of friction.

A drag racer can pull 5 g's. The arc tangent of 5 is around 79 degrees. If you measured the angle from the contact patch under the rear tires to the center of gravity, it would need to be under 12 degrees from the horizontal. [Ignoring aerodynamic effects]

You say that a skater can pull over 1 g. The arc tangent of 1 is 45 degrees. So the lean angle will be over 45 degrees from the vertical. You measure that angle from the contact patch under the skateboard to the position of the center of gravity of the skater plus counterweight.

If a motorcycle can corner at 2 g's then the lean angle will be 64 degrees from the vertical. You measure that angle from the contact patch to the center of gravity of rider plus bike. [Ignoring gyroscopic effects]

 

[Devin-M]

Thank you that is a very informative answer.

 

[Devin-M]

I suggested they hold the battery forward— no weight penalty.

(AI generated)

 

[A.T.]

electric skateboard riders showed me they are getting around 1g acceleration from leaning alone…

I assume the forward lean (weight destitution) controls the electric motor thrust? Your phrasing is really weird. It's like saying: Fighter pilots get 9g acceleration from pulling on a stick alone.

 

[Devin-M]

I assume the forward lean (weight destitution) controls the electric motor thrust? Your phrasing is really weird. It's like saying: Fighter pilots get 9g acceleration from pulling on a stick alone.

The lean angle determines whether the rider gets “bucked off” the board when thrust is applied.

But, assuming the board is rear wheel drive, and the rider’s rear foot is above the rear truck, and the rider lifts front foot off the board during launch, then putting the battery on the rider instead of the board should give the drive wheels more traction before we even consider how it affects the angle from the contact patch to the rider’s center of mass.

 

[A.T.]

I assume the forward lean (weight destitution) controls the electric motor thrust? Your phrasing is really weird. It's like saying: Fighter pilots get 9g acceleration from pulling on a stick alone.

The lean angle determines whether the rider gets “bucked off” the board when thrust is applied.

Does the weight distribution on the axles control the thrust?

 

[Devin-M]

Does the weight distribution on the axles control the thrust?

Yes if the rider is applying as much throttle as possible without getting bucked off.

Also yes if the drive wheel has more traction without the overall vehicle weight increasing, and the rider is applying as much throttle/thrust as possible without getting bucked off the back of the board.

 

[A.T.]

Yes if the rider is applying as much throttle as possible without getting bucked off.

Also yes if the drive wheel has more traction without the overall vehicle weight increasing, and the rider is applying as much throttle/thrust as possible without getting bucked off the back of the board.

How is the rider "applying throttle"?

 

[Devin-M]

How is the rider "applying throttle"?

Thumb throttle:
https://skateboardselectric.com/products/thumb-throttle-remote-verreal-rs

Sort of like a spring loaded volume knob for your thumb, turning it up increases the current in the stator, which increases thrust.

 

[A.T.]

Thumb throttle:
https://skateboardselectric.com/products/thumb-throttle-remote-verreal-rs

electric skateboard riders showed me they are getting around 1g acceleration from leaning alone…

If thrust is controlled by thumb, what do you mean by "getting around 1g acceleration from leaning alone"?