Transfer function question opamp + voltage divider

[Dextrine]

〖 mod note: moved from technical forum, so template is missing 〗
〖 mod note: click on thumbprint image to see legible image 〗

I was wondering if anyone could provide some more insight as to how to find the current through Rc. The first picture TRANSFER1 I can find the current Ic through Rc by the following method:

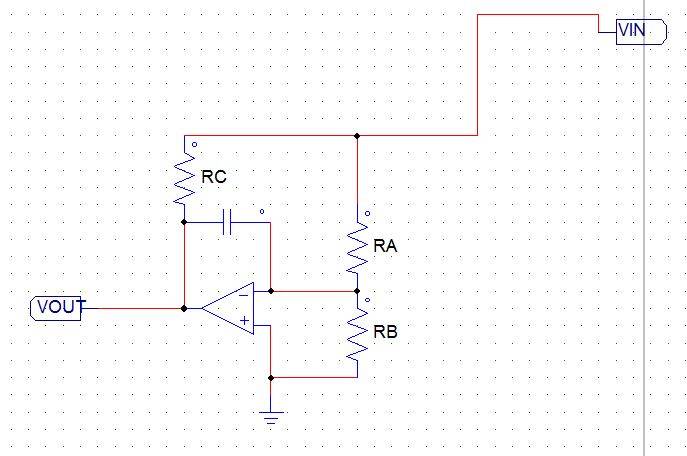
Ic = (Vin - Vout)/Rc
Vout = -Vin(1/(R*s*C))

Ic = Vin(1+1/(R*s*C))

However, if I add a voltage divider network before the input, the problem becomes much more difficult for me here is my latest attempt:

Ic = (Vin - Vout - I1*R1)/Rc
Vout = (-Vin+I1*R1)/(Ra*s*C)

Ic = Vin + (Vin-I1*R1)/(Ra*s*C) - I1*R1.

Now the problem is that this current will be multiplied by CTR from an optocoupler then multiplied by a pullup resistor to get a voltage Vfb on the other end.
There's no way I can think of to write this equation as Vfb/Vin.

I'm essentially modelling a TL431 and an optocoupler per the following: http://www.onsemi.com/pub_link/Collateral/TND381-D.PDF on page 18I appreciate any help and if this is not the appropriate place to post this, please let me know where I can. I'll keep trying and if I figure it out I'll update this post.
Thanks in advance.

 

[Dextrine]

I should have clarified, Ic is the current through Rc.

 

[NascentOxygen]

So you're interested in the current through R_C.

If we denote $v_A$ as the voltage at the node where 4 resistors join, then you have

$i_{R_C}\ =\ \dfrac{v_A\ -\ v_o}{R_C}$

and this leaves you needing to determine $v_o$ in terms of $v_A$ [easy]
and finally $v_A$ in terms of $v_{in}$ [not too difficult].

 

[The Electrician]

Now the problem is that this current will be multiplied by CTR from an optocoupler then multiplied by a pullup resistor to get a voltage Vfb on the other end.
There's no way I can think of to write this equation as Vfb/Vin.

The ON Semi TechNote you linked shows that if you have an expression for Ic, Vfb is just Vfb = CTR*Rpullup*Ic. So if you have an expression for Ic such that Ic/Vin = expr, then Vfb/Vin = CTR*Rpullup*expr; this part is easy.

Regarding your result for Ic when R1 and R2 are added to the circuit, wouldn't you expect R2 to be involved in the result? Since your result doesn't include R2 we know right away it's not correct.

Your result so far: Ic = Vin + (Vin-I1*R1)/(Ra*s*C) - I1*R1 includes I1, which you don't know yet.

With R1 and R2 added, the complexity of the circuit has increased enough that it might be time to use a systematic method of solution. It wouldn't be too hard to just write the node equations and solve for the voltage across Rc in terms of two of the node voltages.

 

[Dextrine]

So you're interested in the current through R_C.

If we denote $v_A$ as the voltage at the node where 4 resistors join, then you have

$i_{R_C}\ =\ \dfrac{v_A\ -\ v_o}{R_C}$

and this leaves you needing to determine $v_o$ in terms of $v_A$ [easy]
and finally $v_A$ in terms of $v_{in}$ [not too difficult].

Luckily, I had gotten to that point as well, however I am having difficulty with finding Va in therms of Vin. Any way you could point me in the right direction? Modeling that first portion as a voltage divider doesn't seem to work either.

 

[The Electrician]

Do you know how to do a nodal analysis? See: https://en.wikipedia.org/wiki/Nodal_analysis

You have 4 nodes so you'll need 4 equations for a nodal analysis.

 

[Dextrine]

Do you know how to do a nodal analysis? See: https://en.wikipedia.org/wiki/Nodal_analysis

You have 4 nodes so you'll need 4 equations for a nodal analysis.

I will definitely look into this thanks!

 

[gneill]

You have 4 nodes so you'll need 4 equations for a nodal analysis.

Have you taken into account the effect that the op-amp has on the potentials at its inputs?

 

[The Electrician]

Have you taken into account the effect that the op-amp has on the potentials at its inputs?

Is this question about the number of nodes?

I'm referring to the OP's image: https://www.physicsforums.com/attachments/transfer2-jpg.111884/

 

[gneill]

Is this question about the number of nodes?

I'm referring to the OP's image: https://www.physicsforums.com/attachments/transfer2-jpg.111884/

Yes.

 

[The Electrician]

I'm not sure how to answer your question. I just looked at the topology of the circuit to determine the number of nodes. I see the input node Vin, the node you designated VA, the minus input, and the Vout node; that's 4 nodes. I am not counting the reference node as is commonly done when enumerating the nodes to be solved.

 

[gneill]

I'm not sure how to answer your question. I just looked at the topology of the circuit to determine the number of nodes. I see the input node Vin, the node you designated VA, the minus input, and the Vout node; that's 4 nodes. I am not counting the reference node as is commonly done when enumerating the nodes to be solved.

I don't want to give too much away until the OP has had a chance to make an attempt, but I'm hinting that the op-amp is going to force the potential difference between its inputs to a certain value that will simplify the analysis. Also, the input will not be an essential node since it's a "fixed" potential offset from the ground reference.

 

[The Electrician]

Even though the input is not an "essential" node, it can still be included in the nodal solution, and to do so can have advantages on occasion.

I know that there may be various ways to simplify solutions to any given problem, but what I suggest to students when the number of nodes begins to increase is this: rather than spend time searching for simplifications, just use a systematic method. Enumerate the nodes and write the node equations.

If there are N nodes, a simplified method may be possible using only N-1 equations. But how much time will be spent looking for the simplification? It might be quicker to write one more node equation, since the writing of node equations is generally easy, and solving simultaneous linear equations is quick in this day and age of computer solvers.

It's good for the beginning student to gain experience in circuit analysis, and looking for simplifications contributes toward that experience. But I think it's also good to consider a systematic method if a simplification isn't apparent fairly soon. That's why I said in post #4 "With R1 and R2 added, the complexity of the circuit has increased enough that it might be time to use a systematic method of solution."

In post #5 he's asking for another nudge which I assume you will give him. I thought It would be good to suggest another method as well.

 

[gneill]

I agree that students should have a systematic method to apply when the way forward is not obvious, and yes, modern solvers make this a practical option. It doesn't help much on exam questions though, where access to computer based solvers may be curtailed.

Students should be able to recognize essential nodes to minimize the number of equations that need to be written. They should also be able recognize and use the properties of the ideal op-amp to their advantage. It takes only a moment to do this preliminary analysis by inspection and can save quite a bit of time and effort in what follows.

 

[The Electrician]

I think he's waiting for the extra nudge from you.

 

[gneill]

I think he's waiting for the extra nudge from you.

I think the OP should be able to take a hint or two from our discussion and try a few things. I'd like to see what he (or she) can do with what's been offered so far. If @Dextrine needs more help then s/he can let us know what problem s/he's run into.

 

[NascentOxygen]

I am having difficulty with finding Va in therms of Vin. Any way you could point me in the right direction?

☝Recognize that R_A has one end earthed (virtual earth).

 

[Dextrine]

I'm here and I'm not waiting for more nudges! I just won't get a chance to try again until tomorrow since I'm kind of busy today. Looking forward to giving it another go.

 

[Dextrine]

Alrighty so after some math, I have the following:
$$I_c = -V_in/R_c*(1/(R_a*C*s-x*R_1*R_a*C*s)-1/(1-x*R_1)) where x = -1/(R_a*R_c*C*s)-1/R_c-1/R_a-1/R_2$$

Hopefully my latex code is ok, can't remember how to use it too well.

 

[The Electrician]

Your latex didn't produce a nice looking result, easily readable by humans; oh, well.

Making the substitution for your auxiliary variable x, I get a reasonably nice looking final expression:

I solved it by doing a full nodal analysis using the 4 nodes:
V1 = Vin
V2 = junction of 4 resistors; also called Va in post #3
V3 = minus input of opamp
V4 = Vout

Then taking the difference V2-V4 (same as Va-Vout) and dividing by Rc, we get an expression for Ic

I get the same thing you got. I actually did this on my HP50g calculator, but to get something I could paste here, I re-did it in Mathematica.

 

[Dextrine]

Nice! Thanks a lot for your help! This is awesome glad I finally got it. Now, one final question (i'm pretty sure my intuition is right but i'll double check by asking you)

I have a transfer function already that I need to multiply by the transfer function of the optocoupler/tl431. The gain of the compensation loop AT the crossover frequency should be the inverse of the plant transfer function AT the crossover frequency right?

 

[The Electrician]

That sounds about right, but it would be necessary to know the details of your full system to know for sure.

 

[Dextrine]

That sounds about right, but it would be necessary to know the details of your full system to know for sure.

Well, I'm basically following along this application note exactly as it is on the paper but replacing its compensation circuit with the tl431 and optocoupler circuit that you helped me find the transfer function of.

http://www.ti.com/general/docs/lit/getliterature.tsp?baseLiteratureNumber=slua560&fileType=pdf

Page 17.

 

[The Electrician]

For me to say more would require me to put in a lot of work studying the full extent of what you're doing. I'm sorry, but I can't devote that much time to the task. Quick to answer questions like the one in this thread I can do. Good luck with your project.

 

[Dextrine]

For me to say more would require me to put in a lot of work studying the full extent of what you're doing. I'm sorry, but I can't devote that much time to the task. Quick to answer questions like the one in this thread I can do. Good luck with your project.

Thanks, no problem at all, you have helped a lot. It was more just a question that, if it was easy to answer, would be cool but I don't expect you to do any deep level of work at all, that's for me to do. Thanks again though!

 

[Dextrine]

Your latex didn't produce a nice looking result, easily readable by humans; oh, well.

Making the substitution for your auxiliary variable x, I get a reasonably nice looking final expression:

View attachment 111972

I solved it by doing a full nodal analysis using the 4 nodes:
V1 = Vin
V2 = junction of 4 resistors; also called Va in post #3
V3 = minus input of opamp
V4 = Vout

Then taking the difference V2-V4 (same as Va-Vout) and dividing by Rc, we get an expression for Ic

View attachment 111974

I get the same thing you got. I actually did this on my HP50g calculator, but to get something I could paste here, I re-did it in Mathematica.

I think your answer might be missing a factor of $$R_1$$ being multiplied by $$R_2*R_A*R_C*C*s$$
I've done and redone the problem using Mathics (like a free mathematica) and keep getting that extra factor of R1 that you don't have.
NEVERMIND I found my error in typing in my values