Why use row reduction to find T's matrix relative to bases B and B'

[jolly_math]

Homework Statement

Let T be the linear transformation from R3 into R2 defined by T(x1, x2, x3) = (x1 + x2, 2x3 - x1).
B={α1,α2,α3} and B′ ={β1,β2}, where α1 = (1,0,−1), α2 = (1,1,1), α3 = (1,0,0), β1 = (0,1), β2 = (1,0). What is the matrix of T relative to the pair B, B′?

Relevant Equations

transformation

T(α1), T(α2), T(α3) written in terms of β1, β2:
Tα1 =(1,−3)
Tα2 =(2,1)
Tα3 =(1,0).
Then there is row reduction:

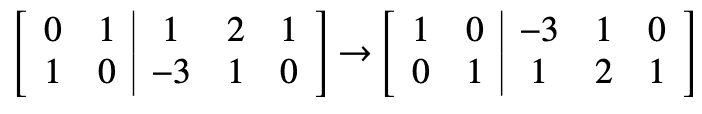
Therefore, the matrix of T relative to the pair B, B' is

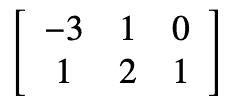
I don't understand why the row reduction takes place? Also, how do these steps relate to $B = S^{-1}AS$? Thank you.

 

[pasmith]

The solution has calculated the matrix of $T$ relative to the basis $B$ and the standard basis of $\mathbb{R}^2$, $\{ e_1 = (1,0), e_2 = (0,1) \}$. But $\beta_1 = e_2$ and $\beta_2 = e_1$ so the rows of that matrix need to be swapped to give the matrix with respect to $B$ and $B'$, But you really don't need row reduction to do that; you can just swap the rows.

If $B'$ depended on the standard basis in a less straightforward manner, then the row reduction may have been necessary to get to the required matrix.