Transient Response RLC: Calculating Vc(t) for a Series Circuit | 9121 Problem

[gmm]

9121. Problem

If we assume that the initial voltage, Vs, is equal to zero, and it rises to five volts at t = 0, derive an expression for the voltage across the capacitor as a function of time. That is, calculate Vc(t)

2. Homework Equations

this is a series RLC so I'm trying to calculate for Vc(t). Also I used α=R/2L

3. Attempt at solving
L= 120 *10^-6 H
C=0.01 *10^-6 F
R= 33 Ω
ωo=1/√(120*.01*10^-12)=912,870
α=33/(2*120*10^-6)= 137,500
α<ωo ∴ this is under-damped
ωd=√(912,870^2 - 137,500^2)=902,456
D1=(0-5)V... because voltage across capacitor at t=0 is 0V
D2=(0 + 137500[0 - 5])/902456= -0.7618... the current and the voltage through the capacitor at t=0 are both zero, because the inductor does not allow the current to change instantaneously.
With this I built my Total
Vc(t) = e^(-137500t)*(-5cos(902456t) - .7618sin(902456t)) + 5

I then simulated the circuit in Multisim with a square wave voltage source of 0 to 5 V.
the transient analysis shows that when the voltage source goes from 0 to 5V the peak voltage at the capacitor goes up to about 8.5V Here is the plot, and a zoom into the first pulse.

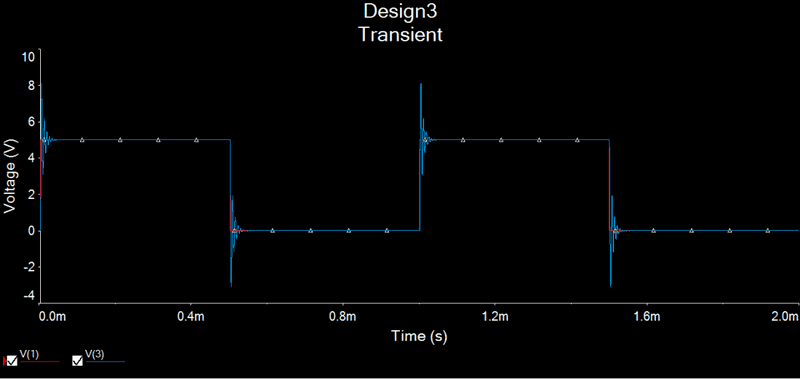
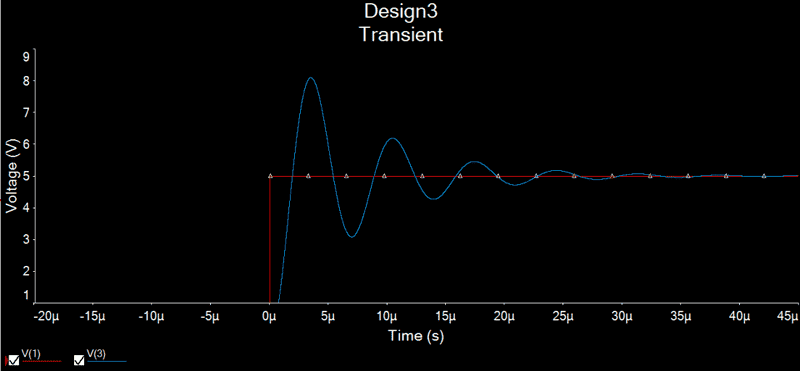
The red is the Source voltage and the blue is the capacitor voltage.
when I plot my Vc(t) it does not resemble this, it gives a lower peak capacitor voltage, Did i mess up in some of the parameters?? Am I missing something?

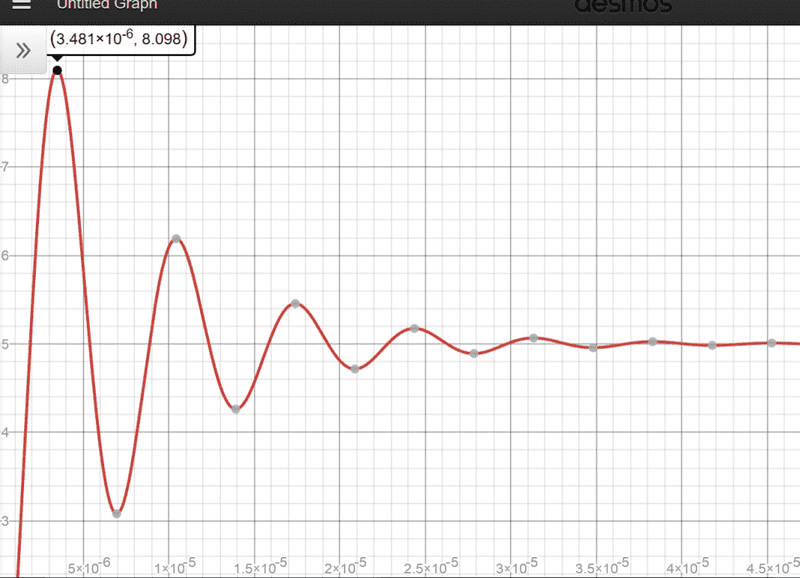
Attached Files:

 

[gneill]

Your calculated plot looks fine to me. I'd be more dubious abut the Multisim accuracy. Simulators are great tools but you need to be a bit careful with them when dealing with high speed transients. See if you can find a simulator menu where you can specify the maximum simulation time step size and play with the value a bit. See what effect it has on the waveform peaks.

 

[gmm]

Your calculated plot looks fine to me. I'd be more dubious abut the Multisim accuracy. Simulators are great tools but you need to be a bit careful with them when dealing with high speed transients. See if you can find a simulator menu where you can specify the maximum simulation time step size and play with the value a bit. See what effect it has on the waveform peaks.

Ah yes. I adjusted my time step size and re-simulated now it's pretty much identical to my model. Thanks qneill