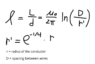- #1
Marcin H
- 306
- 6
This is more of a conceptual question and not a homework question. I am having a hard time understanding why we have to transpose transmission lines and how physically moving them changes anything. Do we only transpose in 3 phase transmission lines when we have 3 wires? Does the orientation matter like equilateral triangle or just 3 next to each other?
I understand that current from one wire can cause a disturbance in the other wire through magnetic flux linkage, but I am having trouble understanding how and why and the details behind it. and why transposing them can solve this issue. I just started learning this material so sorry if I am not making sense.
Moderator: edited to remove the homework template.
I understand that current from one wire can cause a disturbance in the other wire through magnetic flux linkage, but I am having trouble understanding how and why and the details behind it. and why transposing them can solve this issue. I just started learning this material so sorry if I am not making sense.
Moderator: edited to remove the homework template.
Last edited by a moderator: