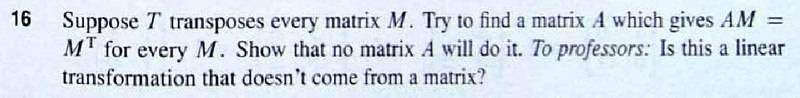This looks to me as mostly a confusion of words. First, "do linear transformations only apply to vectors?". The set of all n by m matrices with the usual addition and scalar multiplication of matrices is a vector space and, in the sense of linear algebra, there is no difference between a "matrix" and a "vector".
sS
Second, the second statement, that "Show no matrix will do it" (map a matrix to its transpose) is incorrect- there is such a matrix but applying it to a vector space of matrices is not the usual matrix multiplication.
To write a linear transformation, from one vector space to another, as a matrix we
1: choose an ordered basis for the both vector spaces.
2: Apply that linear transformation to each basis vector of the first space.
3: Write the result as a linear combination of the basis vectors for the second space.
4: Take the coefficients of each such linear combination as a column for the matrix.
If the two vector spaces are, say, the vector space of two by two matrices, then each such matrix is of the form \begin{bmatrix}a & b \\ c & d \end{bmatrix} and "standard" ordered basis for the vector space is
\{\begin{bmatrix}1 & 0 \\ 0 & 0 \end{bmatrix}, \begin{bmatrix}0 & 1 \\ 0 & 0 \end{bmatrix}, \begin{bmatrix}0 & 0 \\ 1 & 0 \end{bmatrix}, \begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix}\}
That vectors space is four dimensional so the space of linear transformations from it to itself is 4x4= 16 dimensional and a matrix representing any such linear transformation is a 4 by 4 matrix. There is no 2 by 2 matrix such that, multiplied by a 2 by 2 matrix gives its transpose but there is a four by four matrix that, multiplied by the coefficient matrix as given by the ordered basis above, gives the coefficient matrix of its transpose, which is what Linear Algebra says must exist.
In the vector space of two by two matrices, the matrix representing the "transpose" linear transformation is
\begin{bmatrix}1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix}