Trigonometric equation of two sines

[brotherbobby]

Homework Statement

Solve the equation : $\sin m\theta + \sin n\theta = 0$

Relevant Equations

1. If $\sin \theta = \sin \alpha$, where $\alpha$ is the smallest angle possible ($|\alpha| > 0$) the general solution for all the angles $\theta = n\pi + (-1)^n \alpha$.

2. If $\cos \theta = \cos \alpha$, where $\alpha$ is the smallest angle possible ($|\alpha| > 0$) the general solution for all the angles $\theta = 2n\pi \pm \alpha$.

3. $\sin C + \sin D = 2 \sin \frac{C+D}{2}\cos \frac{C-D}{2}$

Given : The equation $\sin m\theta + \sin n\theta = 0$.

Attempt : Using the formula for $\text{sin C + sin D}$ (see Relevant Equation 3 above), the given equation simplifies to

\begin{equation*}
2 \sin \frac{(m+n)\theta}{2} \cos \frac{(m-n)\theta}{2} = 0
\end{equation*}

This implies the following two cases.

(1) $\frac{(m+n)\theta}{2} = k\pi$ where $k \in \mathbb{Z}$ (see Relevant Equation 1 above for sin). This leads to $\boxed{\theta = \frac{2k\pi}{m+n}}$ as the first answer.

(2) $\frac{(m-n)\theta}{2} = 2l\pi$ where $l \in \mathbb{Z}$ (see Relevant Equation 2 above for cosine). This leads to $\boxed{\theta = \frac{4l\pi}{m-n}}$ as the second answer.

I would like to write these out explicitly for various values of integers $k,l$ before I can explore the non-matching of my answers with the one given in the book.

My answer : The values of $\theta$ satisfying the given equation are $\boxed{\theta = \frac{2\pi}{m+n}, \frac{4\pi}{m+n}, \ldots, \frac{4\pi}{m-n}, \frac{8\pi}{m-n}, \ldots}$.

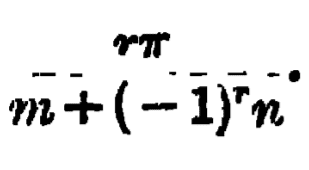Book's answer : Maybe I am right, but have a look at the answer I paste from the book on the right. I rewrite it here for better reading : $\boxed{\mathbf{\theta = \frac{r\pi}{m+(-1)^r n}}}$.

I am assuming that (according to the book) $r \in \mathbb{Z}$. Hence if I begin with $r = 1$, I should have as an answer $\theta = \frac{\pi}{m-n}$! When I substitute this answer in the displayed equation above, which is the same as the given problem written as a product of a sin and a cosise term, I find that it holds! The book is correct. Yet this solution is not one that I found - note that I only have answers as multiples of $4\pi$ for the case where the demonimator is $m-n$.

A help or hint will be welcome.

 

[Office_Shredder]

You're trying to find when cos(x)=0 and when sin(x)=0, and you kind of constructed twice as many solutions for sine as you did cosine. But cosine is just sine shifted, so you should find zeros at the same rate for both of them.Also you said k and l are real numbers, I assume you mean integers. But cos (0) is not equal to 0, so your cosine solutions are also just wrong.

 

[brotherbobby]

You're trying to find when cos(x)=0 and when sin(x)=0, and you kind of constructed twice as many solutions for sine as you did cosine. But cosine is just sine shifted, so you should find zeros at the same rate for both of them.Also you said k and l are real numbers, I assume you mean integers. But cos (0) is not equal to 0, so your cosine solutions are also just wrong.

Thank you. I corrected for the case of $k,l \in \mathbb{Z}$ in the problem, both belonging to integers. It is for the case of the cosine where I made a silly error. I will correct it presently.

 

[brotherbobby]

I correct the last part of my solutions. Thank you for your time.

Attempt : It was found that $\cos \frac{(m-n)\theta}{2} = 0 = \cos \frac{\pi}{2} \Rightarrow \frac{(m-n)\theta}{2} = 2l\pi \pm \frac{\pi}{2}$ where $l \in \mathbb{Z}$. This can be written more compactly : $\boxed{\theta = \frac{(4l\pm 1)}{m-n} \pi}$. Hence the range of values for $\theta$ can be written down as $\boxed{\theta = \frac{2\pi}{m+n}, \frac{4\pi}{m+n}, \ldots, \pm \frac{\pi}{m-n}, \frac{3\pi}{m-n}, \frac{5\pi}{m-n} \ldots}$.

Book's answer : The book gives the answer as $$\boxed{\mathbf{\theta = \frac{r\pi}{m+(-1)^r n}}}$$ We can verify that the list of values of $\theta$ from the book matches those of mine above, were one to write them out for various values of $r \in \mathbb{Z}$. $\mathbf{\huge{\checkmark}}$
A doubt lingers.

I obtained my solutions as $\boxed{\theta = \frac{2k\pi}{m+n}}$ and $\boxed{\theta = \frac{(4l\pm 1)}{m-n} \pi}$.

The book writes them both in a compact form : $$\boxed{\mathbf{\theta = \frac{r\pi}{m+(-1)^r n}}}$$

Can you help me reduce my two-storeyed answer into the (nicer) form of that of the book?

Thank you for your time.

 

[vela]

What about $\cos \frac {3\pi}{2} = 0$?

 

[brotherbobby]

What about $\cos \frac {3\pi}{2} = 0$?

I do not understand what you mean. The angle $3\pi/2$ is not a solution to the problem statement above.
Do you mean why not take $\cos \theta = 0 = \cos 3\pi/2$? We take the lowest value of angle that satisfies the given equation, which in this case is just $\pi/2$ [$\cos \pi/2 = 0$]

 

[vela]

My mistake. I managed to miss all the $\pm$s all over the place.

 

[haruspex]

help me reduce my two-storeyed answer into the (nicer) form of that of the book?

The book's answer for r odd corresponds to your set of solutions in blue, and for r even corresponds to your solutions in red. Won't that do?
It does help to realize that the set {${4l\pm 1}$} is the same the set {${2l+1}$}.

 

[Office_Shredder]

Yeah I also think you should write the cosine solutions as $\frac{\pi}{2} +l\pi$, it reduces the number of cases you have to deal with.

Then it's easy to notice you have solutions of the form $\frac{r\pi}{m\pm n}$ for every r, and the only thing left is to figure out how to express the sign of n as a function of r. $(-1)^r$ or $(-1)^{r+1}$ are pretty common.