SUMMARY
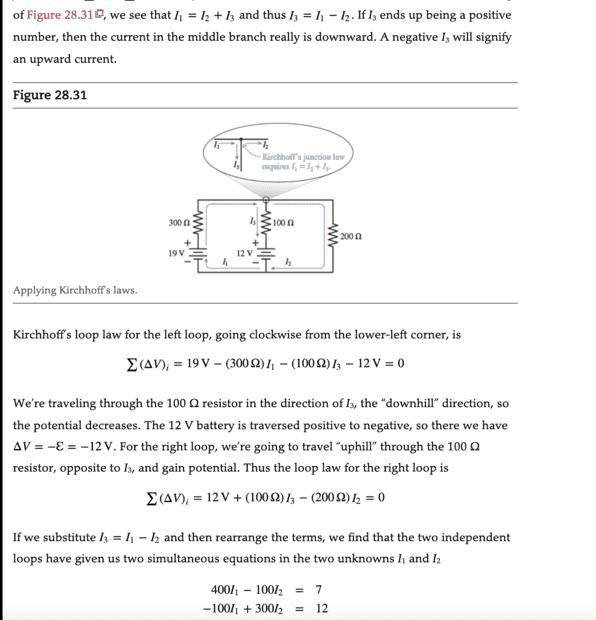
The discussion focuses on solving a circuit problem involving three currents: I1, I2, and I3. The key equation derived is I3 = I1 - I2, which allows for substitution in two given equations to form a system of equations. Participants are encouraged to show their work for specific steps to receive targeted assistance. The method emphasizes the importance of substitution and simplification in circuit analysis.
PREREQUISITES
- Basic understanding of electrical circuits and current flow
- Familiarity with Ohm's Law and Kirchhoff's Current Law
- Ability to manipulate algebraic equations
- Knowledge of circuit analysis techniques
NEXT STEPS
- Study circuit analysis techniques using Kirchhoff's Laws
- Practice solving systems of equations in electrical circuits
- Learn about current division and its applications
- Explore the use of simulation tools like LTspice for circuit analysis
USEFUL FOR
Electrical engineering students, circuit designers, and anyone interested in mastering circuit analysis techniques.