Trouble visualizing what is going on. Volume of object

[Jbreezy]

Homework Statement

Hello,
Here is a link to a pdf .http://www.mrskeller.net/documents/hwsols14.pdf
I'm having issues with number 56. The solution makes no sense to me.

Homework Equations

The Attempt at a Solution

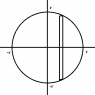
So, I did graph the equation y = sqrt(r^2 - x^2) and I understand that height of the circle. I understand that you need to integrate from -r to r. But I do not understand the integral by any means.

They have $\int 4(r^2-x^2)) dx$ from -r to r
I thought that maybe there were doing something of the form ∏∫y^2 because that is what this chapter uses. But I guess not. They say that the length of a side is 2y = 2sqrt(r^2 - x^2). And the only way that I can see how to get from that equation to the integral they suggest is ly squaring 2y = 2sqrt(r^2 - x^2). So I don't understand that even because if you squared it and used the integral of the form ∏∫y^2 dx then your 4 dissapears. I just don't understand what is going on with this problem. Thanks

 

[eumyang]

The volume of a solid with a known cross section is basically
$${\int_a}^b A(x) dx$$,
where A(x) represents the area of the cross section.

I believe the attached graphic illustrates the problem. Imagine a square lying on its side, the side being the thin rectangle in the diagram. Now imagine a bunch of thin vertical rectangles going from left to right (from -r to r). The distance from the x-axis to the top of this particular rectangle is y. Then you know the length of this thin rectangle (= the length of the square cross section), which is 2y. The area of the square cross section is
$$A = s^2$$
(s is the length of the side),
so plug in 2y for s. Now, what does y equal in terms of x and r? Plug that in for y, and the resulting expression serves as the integrand for this problem.

 

[Jbreezy]

OMG! Thank you that makes a lot more sense. A lot more!