guyvsdcsniper
- 264
- 37
- Homework Statement
- A perfectly elastic spring requires 0.54 J of work to stretch 6 cm from its equilibrium position. (a) What is its spring constant k? (b) How much work is required to stretch it an additional 6 cm? (c) How much work is required to compress the spring 6 cm from its equilibrium position?
- Relevant Equations
- W=1/2kx^2
I do not understand how in part a, the units for K can be N/m. If Work is in joules which is kg*m^2/s^2 and we are diving by x^2 which is m^2, then m^2 should cancel out and we should be left with kg/s^2.
Kg/s^2 makes more sense because in part b when you find the work done you are multiplying kg/s^2 * m^2 which gives you a joule.
Are the units in the work below incorrect? Or am I wrong in my explanation?

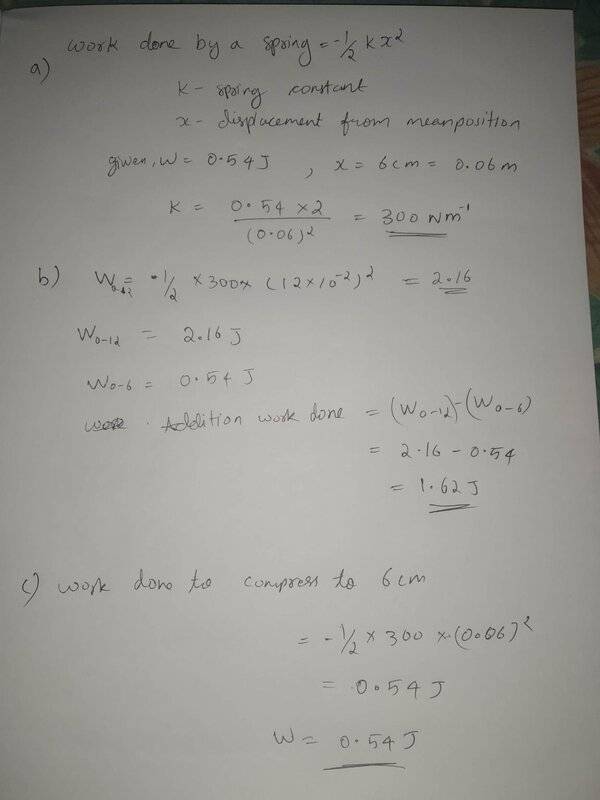
Kg/s^2 makes more sense because in part b when you find the work done you are multiplying kg/s^2 * m^2 which gives you a joule.
Are the units in the work below incorrect? Or am I wrong in my explanation?