Troubleshooting Interplanetary Cruise Calculations

[Viii]

From the rewritten problem: "Q1) What is the minimum total maneuver to slew the spacecraft by 180 degrees?"
Answer: The minimal total maneuver to slew 180 degrees is 180 degrees.
Please be careful in your statement of the problem and do not force us to figure out your calculations just to know what the real question is.

You're right. I wanted to say 'the minimum total maneuver time'. Thanks for pointing that out.

 

[FactChecker]

You're right. I wanted to say 'the minimum total maneuver time'. Thanks for pointing that out.

What made me wonder about minimum time and ask about time available is that it seems as though in interplanetary flight there are months and even years available to get reoriented. A minimum fuel burn would be a tiny burn to get a slow rotation that would give 180 degrees after the total flight time and then a tiny burn to stop that slow rotation.

 

[Viii]

Your rewritten problem in Post #14, still has many issues which make it very hard to understand. Let me try to point-out/explain the issues I can easily spot.

My comments are in square brackets and bold:

Problem: You have a spacecraft the size of a cube (2x2x2 m3, m=3000 kg. It has 24 thrusters (2N each) and one main engine.

[Does this mean there are 4 thrusters on each face of the cube? What direction are they pointing? Do they operate as 2 pairs on each face, to give clockwise or anticlockwise motion about the face’s principle axis? Or maybe their directions can be adjusted.]

The main engine is perpendicular to one of the faces of the cube and each has 4 attitude thrusters.

[Are the ‘attitude thrusters’ the same as the ‘24 thrusters’ previously mentioned?]

For preparing your spacecraft for maneuvers when reaching Mars, you want to rotate it by 180 degrees. For the rotation, you'll use n=4 attitude thrusters per burn.

[I don’t understand which axis the 180 degree rotation is about, which 4 thrusters are used and which directions they fire.]

[Seem like (a) diagram(s) is/are missing?]

Questions:
Q1) What is the minimum total maneuver to slew the spacecraft by 180 degrees? (Assume center of mass is in middle of the cube).

[I guess you have missed out the key word ‘time’!]

Q2) It is given a=0.95 and e=0.85.

[I have no idea what a and e are, though I guess they could relate to absorbtivity and emissivity – in which case shouldn’t they be equal?}

What is the temperature (in Celsius) when reaching Mars, when you know that only one of the faces is illuminated by the Sun and that the heat flow is distrubuted homogeneously?

[Temperature of what? Front face? Back face? Other? Does the cube have any internal heat supply?]

Q3) The power which is generated in the spacecraft can be considered as input power for the radiation balance. How much power (in Watt) should be dissipated inside the spacecraft , in order to achieve 0 Celsius?

[Aha. That suggests Q2 wants you consider the case were internally generated power = 0. Though Q2 doesn’t state this. And what part of the spacecraft should be at 0 ºC? Maybe the centre?]

Note: All formulas and types used in the answers below are provided on slides by my professor.

Answers (what I calculated):
Q1 Answer: In order to find the minimum total maneuver, I firstly used this formula:
tb=sqrt(θmIz/nFL), where

[Formula has appeared by magic!]

tb = durationof burn (sec)
θm = minimum angle of rotation (rad)
[Why minimum? Does it include angular acceleration for half the time and angular deceleration for the other half of the time?]
Iz =moment of inertia around the rotational axis (kg m2)
n = number of thrusters used for the maneuver
F = thrust for each thruster (N)
L = perpendicular distance from the center of mass to the thrust vector (m)
I already have given from the problem that I want to rotate the spacecraft by 180 degrees. So I used θm=180 degrees=pi.
Iz is given by the formula Iz=(2m(b2))/3=8000 kg m2.

[What is ‘b’? What is the axis of rotation?]

n=4 is given.
L=d/2=0.5 m

[The cube is 2m on each side, so it is not clear what d means and what distance 0.5m means.]

[I’ll stop there, as I guess you might now see the problems we face trying to help! Have you given the complete, original, word-for-word problem?]

Answering your questions:
[Does this mean there are 4 thrusters on each face of the cube? What direction are they pointing? Do they operate as 2 pairs on each face, to give clockwise or anticlockwise motion about the face’s principle axis? Or maybe their directions can be adjusted.]

Imagine a cube. Each face has 4 thrusters, yes. They are pointing to the opposite direction of the face (see attached file). I think they operate as 1 pair on each face. But I believe that their directions can be adjusted.

[Are the ‘attitude thrusters’ the same as the ‘24 thrusters’ previously mentioned?]
Yes. They are the same. 24 in total. 4 in each face.

[I don’t understand which axis the 180 degree rotation is about, which 4 thrusters are used and which directions they fire.][Seem like (a) diagram(s) is/are missing?]
Please check the attached file. It's a drawing I did of the shape on the exercise paper. It doesn't state which axis, so I assumed and took the z axis. I also added one similar exercise the professor had in the past (see second attachment please).

[I guess you have missed out the key word ‘time’!]
Yes, I unfortunately did. I'm sorry.

[I have no idea what a and e are, though I guess they could relate to absorbtivity and emissivity – in which case shouldn’t they be equal?}
It is explained in the answers of that post. But to answer and your question here, yes, the are absorbtivity and emissivity. I asked the professor today and he said that they are absorbtivity anf emissivity of a specific material, called black epoxy, which the spacecraft is covered with. (Just to say that he didn't mention this when he gave us the problem).

[Temperature of what? Front face? Back face? Other? Does the cube have any internal heat supply?]
Temperature of the spacecraft , which is covered with black epoxy. I guess we choose which face. No mention for any internal heat supply.

[Aha. That suggests Q2 wants you consider the case were internally generated power = 0. Though Q2 doesn’t state this. And what part of the spacecraft should be at 0 ºC? Maybe the centre?]
Probably something like that. There is nowhere stated what oart should be at 0 Celsius, so is it stupid to assume the entire spacecraft temperature?

[Formula has appeared by magic!]
Somehow. It was given. You can see it also at the second attached file for another exercise, for a 90 degree maneuver.

[What is ‘b’? What is the axis of rotation?]
b is the side of the cube, which is 2. I assumed and took z and that it passes through it's egde.

[The cube is 2m on each side, so it is not clear what d means and what distance 0.5m means.]
d is half the side distance, which is the distance from the center of mass to the trust vector. So d=1. I assumed this also. It's nowhere given.

[I’ll stop there, as I guess you might now see the problems we face trying to help! Have you given the complete, original, word-for-word problem?]
Thank you for your patience. I have given the problem, but I'm so confused now myself.

 

[Viii]

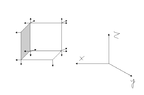
The moment of inertia of a cube depends crucially about what axis you choose.

Which axis do you think is relevant here? Why?This result looks like it derives from one of the SUVAT equations for rotational motion. I am skeptical, however, because it appears to be missing a factor of two. You have not justified this formula in any way.

So let us try to fill in with the justification that you should have provided...

The way to minimize the time needed to obtain a 180 degree rotation is to turn the thrusters on and leave them on until the desired rotation angle has been achieved. We assume that the craft is starting without rotation.

We will accept that the craft will be rotating rapidly at the end of the rotational burn. This is a questionable assumption. If one is trying to maneuver a craft, one would not normally want the craft to remain rotating.

We can start with $\theta=\frac{1}{2}\alpha t^2$ where $\theta$ is the rotation angle (in radians) achieved after $t$ seconds with constant angular acceleration $\alpha$.

We want to solve for the required time $t$. So we divide both sides by $\frac{1}{2}\alpha$ and get $\frac{2 \theta}{\alpha}=t^2$.

Then we flip left for right and take the square root of both sides yielding $t=\sqrt{\frac{2 \theta}{\alpha}}$

What remains is finding $\alpha$ in terms of the moment of inertia of the cube $I_z$, the magnitude of the forces providing the torques $F$, the moment arm for the torques $L$ and the number of forces $n$. The result is that $\alpha=\frac{nFL}{I_z}$.

[Your choice of variable name $\theta_m$ for the rotation angle was poor. Presented in plainish ASCII, $\theta_m$ is shown as θm which looks like angle $\theta$ multiplied by mass $m$. I've chosen to dispense with the m subscript on $\theta$].

In any case, once we substitute in for $\alpha$ in $t=\sqrt{\frac{2 \theta}{\alpha}}$, we get $$t=\sqrt{\frac{2 \theta I_z}{nFL}}$$This does not match your proposed formula: tb=sqrt(θmIz/nFL). As predicted, the latter is missing a factor of two.

Hello. I assumed the z axis. I chose it randomly, since it's not stated anywhere which one shall I take. By the way, love your answer. It's very detailed.

I took the same formula as in the picture attached (it's a similar problem). But now that you made the analysis it makes more sense. It was 90 degrees there, so pi/2, so the 2 factor was probably gone by that. Since now we have 180 degrees, we need the 2 factor. Right?

 

[Viii]

We are given conflicting information:

a) the cube is 2m x 2m x 2m and L is the moment (lever) arm for the thrust; I would have thought L = 2m/2 = 1m [edit: or perhaps √2 m] with respect to the centre of mass;

b) L = d/2 (no idea what ‘d’ is) = 0.5m

I would guess that the missing factor of two is, at least in part, due to incorrectly interpreting the meaning of ‘L’ somewhere,

I considered d=1m so L=d/2=0.5m. Bad mistake.

 

[jbriggs444]

I had asked about the chosen axis of rotation.

Hello. I assumed the z axis. I chose it randomly, since it's not stated anywhere which one shall I take. By the way, love your answer. It's very detailed.

Reading from the attachments...

The first attachment shows a set of coordinate axes (x, y and z) drawn isometrically beside an isometric drawing of a portion of the skeleton of a cube. Unfortunately, the axes are drawn slanted differently from the cube. However we can see that the "z" direction is normal to the "bottom" face of the cube.

So we know the direction that the axis of rotation points -- vertical. But that does not answer the question I was trying to ask.

Are we considering rotation around a vertical axis through the centers of the top and bottom faces?

Are we considering rotation around a vertical axis along the center line of the right hand face?

Are we considering rotation around a vertical axis along one vertical edge?

It matters because the moment of inertia of a cube is different depending on what axis you are using.

I had provided a clickable link with my question. If you had clicked on that link, you would have been taken to a page that gives two different formulas for the moment of inertia of a cube. Let me extract the information from that link and provide it directly here.

I = 1/6 ma² = ma²/6 when the axis of rotation passes through the center
I = 2 mb² / 3 when the axis of rotation passes through its edge

Way back in the original post in this thread, you wrote that the moment of inertia of a cube is:
"Iz=(2*m*(b^2))/3". That looks very much like the second of the formulas above.

That means that it is the wrong formula. Because it assumes the wrong axis of rotation.

 

[jbriggs444]

Since now we have 180 degrees, we need the 2 factor. Right?

Yes, if we are solving for the time required to accelerate all the way through 180 degrees then the angle $\theta$ is $\pi$ and we need the factor of two in the formula.

 

[Viii]

I had asked about the chosen axis of rotation.

Reading from the attachments...

The first attachment shows a set of coordinate axes (x, y and z) drawn isometrically beside an isometric drawing of a portion of the skeleton of a cube. Unfortunately, the axes are drawn slanted differently from the cube. However we can see that the "z" direction is normal to the "bottom" face of the cube.

So we know the direction that the axis of rotation points -- vertical. But that does not answer the question I was trying to ask.

Are we considering rotation around a vertical axis through the centers of the top and bottom faces?

Are we considering rotation around a vertical axis along the center line of the right hand face?

Are we considering rotation around a vertical axis along one vertical edge?

It matters because the moment of inertia of a cube is different depending on what axis you are using.

I had provided a clickable link with my question. If you had clicked on that link, you would have been taken to a page that gives two different formulas for the moment of inertia of a cube. Let me extract the information from that link and provide it directly here.
Way back in the original post in this thread, you wrote that the moment of inertia of a cube is:
"Iz=(2*m*(b^2))/3". That looks very much like the second of the formulas above.

That means that it is the wrong formula. Because it assumes the wrong axis of rotation.

You're right. I had the wrong formula all this time. Thank you!

 

[jonagad]

Hello Viii, I would like to know what are your correct answers for this problem

 

[berkeman]

Hello Viii, I would like to know what are your correct answers for this problem

Do you have the same problem in your homework?

 

[jonagad]

Do you have the same problem in your homework?

Hello, yes, it's the same problem, but my answers are different from the ones that viii obtained, so I would like to know which ones are the right ones

 

[jonagad]

I understand that the moment of inertia is I=1/6 ma2 = ma2/6, where m= 3000kg, and a=2m, that gives a value of 2000m² for the moment of inertia, the, when applying the formula for t=sqrt(2*θ*Iz/n*F*L), where θ=180 degrees=pi, Iz=2000 m², n=4 (because you will use four attitude thrusters per burn, F=2 N, L=1m, that gives a value of 39.633 s, then, this "t" that you just obtained is the t_b: time per burn, but you want to know the maneuver time, so, as there are 4 thrusters per burn, then you just have to multiplie the time per burn for the number of thrusters per burn, this gives a total of 158.3 s, but it its incorrect.

Now for the second question, i think there´s an error, the An (area perpendicular to the sun) its not 2, its 4, its the area of a square, then replacing this new An, the temperature gives a value of 260.42 K, or -13.15 °C.

As for the 3rd question, i don´t get why is wrong, but i think i might have an idea, can it the the answer it´s the substraction of the initial Pe (Power emited) that you have with the temperature that you obtained in the second question and the one that you calculated for T=0?