SUMMARY
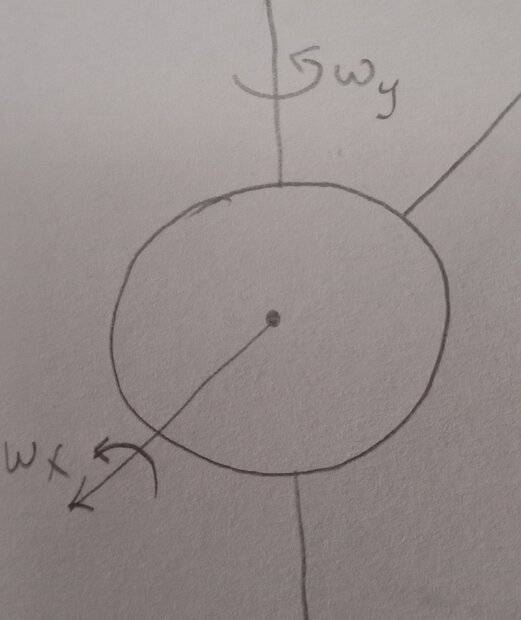
The discussion centers on the dynamics of a disc that can rotate about two perpendicular axes fixed to its body. When attempting simultaneous rotation about these axes, the resulting motion is complex due to the interaction of angular velocities and the inertia tensor. The angular velocity is expressed as ##\boldsymbol{\omega} = \mathbf{i} \omega_x + \mathbf{j} \omega_y##, where the axes are functions of time. The Euler equations are crucial for understanding the motion, particularly in the context of rigid body dynamics.
PREREQUISITES
- Understanding of rigid body dynamics
- Familiarity with angular velocity and inertia tensor concepts
- Knowledge of Euler equations in rotational motion
- Basic grasp of torque and its effects on rotational systems
NEXT STEPS
- Study the derivation and application of the Euler equations in rigid body dynamics
- Learn about the properties of the inertia tensor and its eigenvectors
- Explore the concept of torque and its role in rotational motion
- Investigate the relationship between angular momentum and angular velocity in dynamic systems
USEFUL FOR
Physics students, mechanical engineers, and anyone involved in the study of rotational dynamics and rigid body motion will benefit from this discussion.