Tunneling from Rectangular barrier - Exponential Decay ?

[svrphy]

Tunneling from Rectangular barrier - Exponential Decay ??

Consider the Rectangular Potential Barrier. If one solves bound state Problem in this case, wavefunctions of Exponentially Decaying and rising kind are found for the Region in the Barrier.
ψ = A e^αx + B e^-αx

Yet Most Books and internet sources state that the Wavefunction in the Region is just Exponentially Decaying. From Wikipedia :

Note that, if the energy of the particle is below the barrier height, k_1 becomes imaginary and the wave function is exponentially decaying within the barrier (en.wikipedia.org/wiki/Rectangular_potential_barrier)

From Hyperphysics:

But the wavefunction associated with a free particle must be continuous at the barrier and will show an exponential decay inside the barrier. (http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/barr.html)

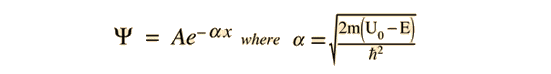
Simulation here : http://www.st-andrews.ac.uk/physics/quvis/embed_item_3.php?anim_id=16&file_sys=index_phys

I just can't Understand these apperent Double Standards here. The wavefunction is assumed to be "Exponentially Decaying inside the Barrier". At the same time, the Exponentially Rising term is inevitably used in the derivation of tunneling probabilities.

Just what is Going on ??

 

[Avodyne]

The rectangular potential barrier does not have bound states, so I'm not sure what you mean by "If one solves bound state Problem in this case".

If you consider the reflection/transmission problem, it is true that, inside the barrier, both rising and falling exponentials must be included. However, in the case where $\alpha a\gg 1$, the coefficient of the rising exponential is smaller than the coefficient of the falling exponential by a factor of approximately $\exp(-2\alpha a)$, where $a$ is the width of the barrier. This means that the wave function inside the barrier is very well approximated by a strictly falling exponential.

 

[svrphy]

The rectangular potential barrier does not have bound states, so I'm not sure what you mean by "If one solves bound state Problem in this case".

Really sorry for that wrong piece of terminology. Yes, I indeed was referring to Reflection/Transmission Problem. Could you elaborate on the consideration of αa>>1 ? Does it come about when boundary conditions are applied ??

 

[jtbell]

Suppose αa = 1000. How does e¹⁰⁰⁰ compare to e^-1000?

For more detail, look up the actual result for the transmission probability, which you can find on Wikipedia:

http://en.wikipedia.org/wiki/Rectangular_potential_barrier

Scroll down to the section "Analysis of the obtained expressions", subsection E < V₀, and look at the formula for T. The two exponentials we're talking about are buried inside the sinh(k₁a) piece. (Look up the definition of sinh(x) if you need a reminder.)

For a very "thin" barrier, both exponentials do contribute significantly to the result; but in many cases we get a very good approximation by ignoring the negative exponential. In that case the exact solution reduces to the one in Hyperphysics as an approximation.

 

[Avodyne]

Set up the problem:
$$\psi(x)=e^{ikx}+R e^{-ikx},\ \ x<0$$
$$\psi(x)=A e^{\alpha x}+B e^{-\alpha x},\ \ 0<x<a$$
$$\psi(x)=T e^{ikx},\ \ x>a$$
Require $\psi(x)$ and $\psi'(x)$ to be continuous at $x=0$ and $x=a$. You will find
$${A\over B}={\alpha+i k\over \alpha-ik}\,e^{-2\alpha a}.$$

 

[Jilang]

Ah ha! So both terms in the second line are actually falling exponentials?