Two-Dimensional Springs: Potential Energy and Force Analysis

[ch010308]

Homework Statement

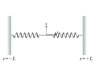
The ends of two identical springs are connected. Their unstretched lengths l are negligibly small and each has spring constant k. After being connected, both springs are stretched an amount L and their free ends are anchored at y=0 and x= (plus minus)L as shown (Intro 1 figure) . The point where the springs are connected to each other is now pulled to the position (x,y). Assume that (x,y) lies in the first quadrant.

a) What is the potential energy of the two-spring system after the point of connection has been moved to position (x,y)? Keep in mind that the unstretched length of each spring l is much less than L and can be ignored.
Express the potential in terms of k, x, y, and L.

b) Find the force F on the junction point, the point where the two springs are attached to each other.
Express F as a vector in terms of the unit vectors x and y.

Homework Equations

F=kx

The Attempt at a Solution

I don't quite understand how to approach this problem. Do we treat the 2 springs as a single system or 2 springs? Wouldn't the springs stretch by different lengths if the center point is pulled in (x,y) direction?

Any help would be great! Thanks!

 

[Doc Al]

Wouldn't the springs stretch by different lengths if the center point is pulled in (x,y) direction?

Sure. So find the potential energy of each spring separately, then add to get the total.

 

[makeAwish]

I have this problem as well. I can only solve part one.

For second part,

my force for the string on the left (lets say force1) = kx1(cos angle1)i + kx1(sin angle1)j
and
my force for the string on the right (lets say force2) = kx2(cos angle2)i + kx2(sin angle2)j

then sub in the cos angles and sin angles,

my total force is 2kLi + 2kyj

note: my i and j are the unit vectors.

but the answer is wrong. it is independent of L..

Pls help! Thanks!

 

[makeAwish]

are my directions correct??
is it supposed to be negative??

 

[zSuperkz]

I think it should be -2kxi-2kyj

 

[Phrak]

What in the blue blazed does a negligable unstretched length mean? I guess the springs in the drawing are of the non l-type.

 

[makeAwish]

I think it should be -2kxi-2kyj

why is it x instead of L?

i can understand that it is negative, but i can't figure out the x..

 

[Doc Al]

my force for the string on the left (lets say force1) = kx1(cos angle1)i + kx1(sin angle1)j
and
my force for the string on the right (lets say force2) = kx2(cos angle2)i + kx2(sin angle2)j

Spell out the details of your calculation, paying attention to signs.

 

[makeAwish]

yeah now i have -2xLi - 2kyj
but how to get rid of L?

 

[Doc Al]

yeah now i have -2xLi - 2kyj
but how to get rid of L?

The only way to tell where you went wrong is for you to show the details of your calculation.

 

[Dr.D]

The force in the spring depends on the elongation of the spring. After the connection point moves to (x,y), the spring on the left has length
LL = sqrt((L+x)^2+y^2)
and the spring on the right has length
LR = sqrt((L-X)^2+y^2)
The original, free length of each spring was zero (not very realistic, but that is what the problem said)
Therefore the force in the spring on the left is FL = k*LL and on the right FR = k*LR, speaking in terms of magnitudes only.

From this point it should be easy to complete both parts of the problem.

 

[ch010308]

I can solved the question already! Thank you all for helping!

 

[electricblue]

The force in the spring depends on the elongation of the spring. After the connection point moves to (x,y), the spring on the left has length
LL = sqrt((L+x)^2+y^2)
and the spring on the right has length
LR = sqrt((L-X)^2+y^2)
The original, free length of each spring was zero (not very realistic, but that is what the problem said)
Therefore the force in the spring on the left is FL = k*LL and on the right FR = k*LR, speaking in terms of magnitudes only.

From this point it should be easy to complete both parts of the problem.

please correct me if i am wrong here..
so i found the force acting on the left spring and right spring..

to find U, it means i have to sum the total work done by both springs?
in this case, i should integrate FL and FR over the displacement right?

but what should be limits of this integration(i am confused due to x and y components of the question)?

 

[Doc Al]

to find U, it means i have to sum the total work done by both springs?
in this case, i should integrate FL and FR over the displacement right?

but what should be limits of this integration(i am confused due to x and y components of the question)?

That's the hard way. You must have found the stretch in each spring as a function of x & y. What's the potential energy of a stretched spring? Just find the potential energy of each spring, then add to get the total.

 

[Dr.D]

The limits of integration for the FL integration are 0 to LL and for the FR integration 0 to LR. Remember that the variable of integration is the stretch, not x or y directly.

 

[makeAwish]

The only way to tell where you went wrong is for you to show the details of your calculation.

my resultant force,
Fr = F1 + F2
= -[(kx1 cos angle 1) + (kx2 cos angle 2)] i - [(kx1 sin angle 1 + kx2 sin angle 2)] j
= - (kL + kx + kL - kx) i - (ky + ky) j
= -2kL i - 2ky j


where i and j are unit vectors..

 

[Doc Al]

my resultant force,
Fr = F1 + F2
= -[(kx1 cos angle 1) + (kx2 cos angle 2)] i - [(kx1 sin angle 1 + kx2 sin angle 2)] j

The problem is with the sign of your x-components. The springs pull in opposite directions along the x-axis, so the x-components of their forces will have opposite signs.

 

[makeAwish]

The problem is with the sign of your x-components. The springs pull in opposite directions along the x-axis, so the x-components of their forces will have opposite signs.

yeah, i saw my mistake! haha. thank you! :)

but can i ask sth? cos initially i tot the (cos angle) and (sin angle) in the eqn will take care of the directions, so we just put all positive. it doesn't work tat way?

 

[Doc Al]

but can i ask sth? cos initially i tot the (cos angle) and (sin angle) in the eqn will take care of the directions, so we just put all positive. it doesn't work tat way?

Sure, if you use the correct angle. Don't confuse θ with θ + 180°. And you still need to use the correct direction of the force vector.

 

[makeAwish]

Sure, if you use the correct angle. Don't confuse θ with θ + 180°. And you still need to use the correct direction of the force vector.

hmm. anyway in this qns, the angles are all less than 90 degrees, so their cos and sin will still be positive right?

is it like everytime we deal with such qns, no matter the cos and sin angle will turn out positive or negative, we also need to include the direction of the force vector?

 

[Doc Al]

For problems like this I generally choose angles less than 90 and attach the correct sign as needed by hand. But if you want the sine and cosine to do the work of giving it the proper sign, then you must always measure your angles with respect to the positive x-axis. (Note that angles are measured counterclockwise from the axis.) In this problem, the angles that the force vectors make with the positive x-axis are both greater than 180.

 

[makeAwish]

ah.. okay! i think i know le. thanks :)

 

[makeAwish]

do u mind helping me see my the other qns? the disk rotating problem..

thanks a lot.

 

[Doc Al]

I'll be away for a few hours, but I'll take a look when I return.