Two eccentric flywheels run on same axis

[tarakan]

I was asked to build an experimental setup for one of my friends and I did it successfully.

The setup included two eccentric flywheels, spinning in opposite directions on the shafts of two stepper motors that were facing each other. I 3D printed a pair of identical eccentric flywheels and pressed them on the shafts of the stepper motors.

Those eccentric flywheels generated oscillations that canceled each other out at some angles.I became obsessed with a problem that I cannot solve.

I want to make sure that the eccentrics are causing oscillations on the same plane so no rotational vibrations are created.
At least I want the system to approach that state.

See illustration:

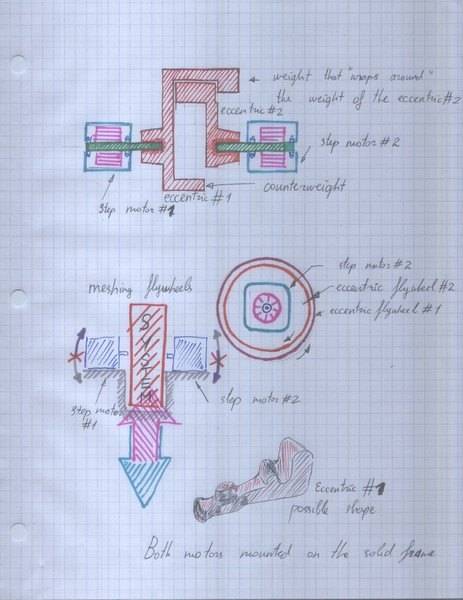
I know that making one big eccentric flywheel with a counterweight wrap itself around the smaller one is the solution. It will involve a lot of calculus.

I am not even sure in what plane I need to integrate my even density eccentrics.

The ability of each eccentric flywheel to create oscillations of the device frame should be equal over a wide range of speeds. (RPMs)

Each eccentric needs to create the same set of forces against the bearings of the motors at the same angles. The only problem is that if they were made identical, they would collide on their paths. So one eccentric flywheel mass has to wrap around the other and use a counterweight to compensate for a greater diameter.

I am not very sure how to describe the problem even. Being obsessive-compulsive I tried to solve this problem in several ways but I cannot clearly define all the variables.

My pair of counter rotating flywheels needs to have equal characteristics over a wide range of rotation speeds, while creating a maximum amount of oscillation forces along the center line of the device.

Thank you.

 

[Baluncore]

For minimum vertical vibration, the centres of mass must move symmetrically on the vertical axis. If the motors are counter-rotating then the heavy sides that were in opposition will have to pass on the same side 90° later, which must result in a horizontal imbalance.

Some balancing challenges are impossible. By varying the relative phase of the motors, you can adjust the direction of the imbalance, but with a pair of counter-rotating motors, you can never vary the amplitude or make it zero.

 

[tarakan]

I am talking about Rotational vibration cancellation.

For minimum vertical vibration, the centres of mass must move symmetrically on the vertical axis. If the motors are counter-rotating then the heavy sides that were in opposition will have to pass on the same side 90° later, which must result in a horizontal imbalance.

Some balancing challenges are impossible. By varying the relative phase of the motors, you can adjust the direction of the imbalance, but with a pair of counter-rotating motors, you can never vary the amplitude or make it zero.

I want to exclude the angular rotations from two flywheels being slightly off center. Or minimize them.
The idea is to make most of the mass of one flywheel surround most of the mass of another flywheel.

So their masses spin along the same plane, mostly. Since one flywheel will have to be bigger than the other, it will require a counterweight portion.

How can I do the math? Thank you.

 

[Baluncore]

I think the counterweight is a distraction, counter productive and not needed.

The requirement is that the eccentric moments of inertia be the same. If one has a centre of mass further from the axis then it does not need as much mass to generate the balancing force.

Think of the motors as having disc rotors of different radii, with a mass attached near the circumference that has the form of a small rectangular part of the wall of a cylindrical tube having the same diameter as the disc.

The length and breadth of that weight will set the inertia when multiplied by the radius. The distance between the discs is set so only the thickness or angular length of the masses need to be calculated.

By making the weights trapezoidal, wide end away from the supporting disk, rather than rectangular, you can move the centre of mass onto the exact midplane of the motors. You could eliminate much of the disc area, but then you must calculate the inertia of the remaining part and sum it's component with the weights.

http://en.wikipedia.org/wiki/Moment_of_inertia#Angular_momentum_in_planar_movement

 

[tarakan]

Maybe I don't need a counterweight. Would it still cause the flywheels to act the same throughout the range of speeds? What about the fact that the system will be allowed to vibrate and that the eccentrics will not rotate about exactly around a center point?

They will rotate around some point between the center point and the center of gravity. This system will not be bolted solid but will rest on springs.

 

[tarakan]

I am trying to do math but I cannot tie abstract formulas from Wikipedia to the problem I am solving. It is too difficult. I know what those formulas stand for and I know what I want to find but I don't know how to connect the two.