SUMMARY
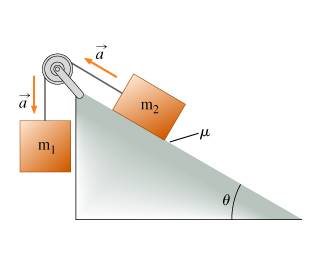
The discussion focuses on calculating the mass ratio \( m_1/m_2 \) for two blocks connected over a frictionless pulley, with block 2 on an inclined plane experiencing kinetic friction. The equations of motion derived are \( m_1g - T = m_1a \) and \( T - m_2gsin(\theta) - \mu m_2gcos(\theta) = m_2a \). The correct mass ratio is given by the formula \( m_1/m_2 = (g(sin(\theta) + \mu cos(\theta) + a))/(g - a) \). Participants identified a missing term in the numerator during the calculation, which was crucial for arriving at the correct solution.
PREREQUISITES
- Understanding of Newton's laws of motion
- Familiarity with inclined plane dynamics
- Knowledge of kinetic friction and its coefficient
- Basic algebra for solving equations
NEXT STEPS
- Study the principles of Newton's second law in multi-body systems
- Learn about inclined plane physics and frictional forces
- Explore the derivation of equations of motion for connected bodies
- Investigate common mistakes in solving physics problems involving pulleys and friction
USEFUL FOR
Students of physics, educators teaching mechanics, and anyone interested in solving problems related to dynamics and friction in multi-body systems.