Two questions about op amps I've troubled for some time.

[Lajka]

Hi,

I was hoping someone could help me resolve a little difficulty I have.

------
Question number one: Say you have an op amp with a negative feedback. I've been taught that the principle of 'virtual ground' must hold. But what happens for a circuit for like this?

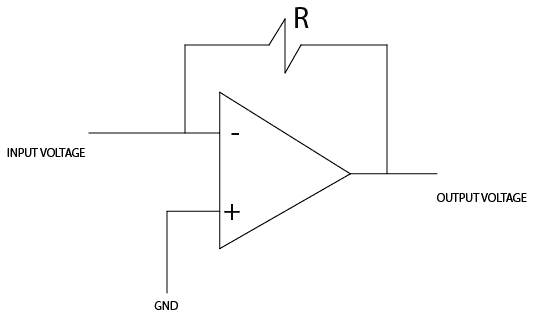
As you can see, I intentionally made the other resistor zero in this configuration (invertible amplifier), so I could force voltage directly into the op amps input. It also makes the gain of this circuit infinite. I understand this is not something that can happen in reality, but from a theoretical point of view, how would you analyze this problem? Is the concept of the virtual ground still valid? If it is, I don't see how.
I still consider this to be the case of a negative feedback, as the portion of the output is brought back into the negative input.

------
Question number two: I have a problem with the way people analyze positive feedback. For example, consider this slide from the presentation. I see absolutely no reason why would anything change if I would just switch the plus and the minus sign on the op amp, and thus go from negative to positive feedback. Following that logic, I would get my virtual ground even with a positive feedback.

Conceptually, I understand how both negative and positive feedback work. However, I would like to prove myself mathematically that negative feedback forces the inputs to be equal, and positive feedback forces the op amp to go into saturation. I don't know how to do that. If I use the general model, something like:

I could write that:
A = A/(Aβ + 1) for negative feedback;
A = A/(Aβ - 1) for positive feedback.
I don't what to make of that, though. I see no insight in these equations, just new values for gains, respectively.

So, any help about these two questions would be immensely appreciated. Thanks!

 

[yungman]

Let me answer the first question. The virtue ground is established if the input is in current form, and the current is limited by the value of the feedback resistor shown and the maximum voltage swing of the output of the opamp. For example if the output can only swing +/-10V and the feedback resistor is 1K, the maximum current sink and source at the negative input of the opamp by the output is 10mA. Any current driving in or pulling out from the -ve input junction that is less than 10mA, the opamp is able to keep it at virtue ground level, anything more, the junction will go off the virtue ground level. Don't take the "virtue ground" that literal. It only hold if the current is within the limit.

As in your example, if you use a voltage source ( low output impedance) to drive direct into the -ve input junction, you drive it off virtue ground right away as soon as you overcome the current limit as I described above.the second part of your question, if you switch to positive feedback, if you put a slight +ve voltage at Vin, before the output can even react, the voltage at the +ve input will be

V_{diff}=V_{in}\frac{R_2}{R_1+R_2}

So the input goes a little positive. Since the opamp has infinite differential gain, a little +ve and the +ve input will cause the output to swing +ve. As output swing positive, the voltage at the input goes even more positive from the voltage divider of R1 and R2. So this become a positive feedback. So it will continue to goes positive until the opamp reach the maximum +ve and hang there. Don't try to do math, it's just that simple. You cannot just turn one value in your equation. That equation only work if it is negative feedback.

 

[I like Serena]

Hi Lajka! Happy new year! Question 1

The working of an op-amp is actually as follows:
$$V_{out}=(V_+ - V_-)A_{OL}, \qquad\textrm{but limited to $V_{S+}$ and $V_{S-}$}$$
where $A_{OL}$ is the open-loop-gain which is typically ~10⁶ but in practice treated as ∞.
And where $V_{S+}$ and $V_{S-}$ are the positive and negative power supplies.

In your example, suppose you have a $V_{in}$ of -1 V and you have power supplies of ±15 V.
Then your op-amp would saturate and yield $V_{out}=15 V$.
And you would have a current through your resistor with a voltage drop of 16 V.

 

[AlephZero]

The idea of "virtual ground" only applies exactly to an ideal op amp wth infinite gain.

For a real op amp, of course you can force the two inputs to be at different voltage. Just connect a battery between them! If you do that the behaviour of the op amp is nonlinear so none of the assumputions about linear op amps and virtual ground are relevant.

Op amp circuits with two inputs at different voltages are useful, for example as voltage comparators. The output voltage will be close to one of the supply voltages V+ or V- depending on which input voltage is higher.

For your question about feedback, your the feedback equations are assuming the gain A is finite and so the two inputs will not be at exactly the same potential, for either positive or negative feedback.

The main "insight" from the equations is that when A is very large the gain with feedback depends on mostly on \beta, not on the exact value of A. For example work out the gain when \beta = 0.1 if A = 1000, 10,000, or 1,000,000.

 

[I like Serena]

Question 2

You refer to 2 cases here, one is an op-amp with negative feedback, and the other is with positive feedback.

Your slide makes the assumption that the circuit is stable and that the op-amp is not saturated.
Under this assumption, V- equal to ground is a mathematical solution for both negative and positive feedback.
For negative feedback this is a stable solution, but for positive feedback this is an unstable solution (see below for more details).

You can also solve the circuit under the assumption that it is saturated in either the negative or the positive power supply voltage.
With the proper condition on the input voltage these will be stable solutions.Now suppose V- starts at ground voltage, which is a mathematical solution in both cases.
And suppose V- deviates slightly from ground, perhaps caused by noise or by temperature drift.
With negative feedback the resulting output voltage will be opposite to the deviation, effectively steering V- back to ground.
But with positive feedback the output will be in the same direction as the deviation, effectively steering the op-amp into saturation, which is another solution.

 

[jim hardy]

I could write that:
A = A/(Aβ + 1) for negative feedback;
A = A/(Aβ - 1) for positive feedback.
I don't what to make of that, though. I see no insight in these equations, just new values for gains, respectively.

see if this helps:

let me re-phrase them
a = gain with no feedback, AND
GAIN(_fb) = gain with feedback, positive(pfb) or negative(nfb)
here's your equations:
GAIN(nfb) = a/(ab+1) ;;; negative fb
and
GAIN(pfb) = a/(ab-1) ;;;, positive fb

for SIMPLICITY set a = 1

and find limit of gain as b approaches 1

b, GAIN(nfb), GAIN(pfb)
0,,, 1,,,,,,,,, -1

.25,, 0.8,,, -1.33

.5,,, 0.67,,, -2

.75, 0.57,,, -4

.999, .5+,,-1000

1,,,,, 0.5,, -infinity

so with infinite gain it can make an output if input is zero. that's why with feedback you can oscillate.

now make a and b complex numbers ...
if they make denominator into a quadratic with real roots(ie that resolves to zero), it'll probably oscillate.