Types of Rotations - Hi Everybody, Ask Your Questions Here

[Adrian555]

Hi everybody,

This is my first post, so I apologise for all the possible mistakes that I can make now and in the future. I promise that I'll learn from them!

My question is the following: It's well-known the relationship between two pair of cartesian axes when a circular rotation is made:

Nevertheless, when dealing with a Minkowski rotation like this one:

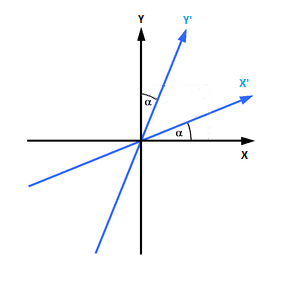
I was wondering if a relationship between the new (blue) and old (black) pair of axis as function of the circular angle alpha can be obtained (that is to say, without using an hyperbolic angle).

Thanks in advance for your help.

 

[mfb]

A relationship similar to the equations above?
Sure. Just use trigonometry: find vectors that correspond to the new axes (x', y') expressed in the old coordinate system (x and y), then find a way to express an arbitrary point on the plane (given in the old coordinates) in the new coordinates. It is a linear equation system.
Alternatively, start with a point given in the new system and transform back to the old one. That gives the same equations but written in a different way.

 

[Adrian555]

First of all, thanks for your answer, I really appreciate your quick response.

So, if I have understood well, the first thing I have to do is to represent a vector and relate its components in both coordinate systems using trigonometry:

But, what should I do now? I'm a little confused...

 

[mfb]

If you convert that sketch to formulas, you get something equivalent to the formulas for the rotation in the first picture.
If that is not what you are looking for, I don't understand the question.

 

[zinq]

There are two closely related concepts that it is essential to keep separated:

a) Rotating points in a fixed coordinate system and expressing their new positions in that coordinate system in terms of the old points and the angle of rotation;

b) Keeping points in a fixed position in some coordinate system but expressing them in terms of a new, rotated coordinate system.

Although the formulas for these two things are very similar, they are distinct concepts and should not be confused with each other.

 

[Adrian555]

Thank you for your replies! My question now is related to the previous one, but has changed. Suppossing that we have the following situation:

According to the picture, we have a vector in an orthogonal frame (with coordinates 2, 2). I want to obtain the contravariant (green) and covariant (blue) components in a new frame where the axes have been rotated an hyperbolic angle alpha.

I have checked that the contravariant components can be obtained as follows:

\begin{bmatrix}{a^1}\\{a^2}\end{bmatrix}=\begin{bmatrix}{cosh(\alpha)}&{-sinh(\alpha)}\\{-sinh(\alpha)}&{cosh(\alpha)}\end{bmatrix}\begin{bmatrix}{a_x}}\\{a_y}\end{bmatrix}

My question is, which is the expression to obtain the covariant components? Maybe I should use the inverse matrix?

\begin{bmatrix}{a_1}\\{a_2}\end{bmatrix}=\begin{bmatrix}{cosh(\alpha)}&{sinh(\alpha)}\\{sinh(\alpha)}&{cosh(\alpha)}\end{bmatrix}\begin{bmatrix}{a_x}\\{a_y}\end{bmatrix}

Thanks for your help.