Understanding Accelerating Pulley Systems: Tension, Forces, and Analysis

[Alan Sammarone]

Hello. I am having some trouble to understand conceptually the behaviour of such a system:

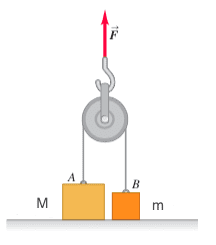
So, both blocks are in contact with the floor, one has mass M and the other has mass m. Then we apply an upwards force F on the axel of the pulley. How does the system behave?

My initial thought is that if

$$ \vec{F} > (m + M)g $$

Then the whole system accelerates upwards. If that's not the case, then only the lighter mass would accelerate (upwards).

That doesn't seem to be case. Particularly, it seems that i should consider that the tension in the string is half the applied force. In general, any pulley attached to a ceiling is going to exert double the tension force on the ceiling. Why is that?So, my question is: how should i go about analysing the behaviour of this system, conceptually, and why? And why is the tension half the force the pulley experiences (if that's even true)?

Thanks!

(This is my first post here. This is not a Homework question, but it was in a book that I've been studying. If I've posted that in the wrong place, i am sorry)

 

[Buzz Bloom]

Hi Samarone:

There are some missing facts from the problem statement, and some assumptions are needed to deal with that.
1. Assume the weight of the pulley, the hook, and the rope/wire connected to the weights are negligible.
2. Assume the frictional force of the rope/wire with the pulley is negligible.

You have already solved the problem if F ≤ (M+m)g: nothing happens.

There are three parts of the motion to solve:
a. How do the hook and pulley behave?
b. How does the M weight behave?
c. How does the m weight behave?

For each of these three, work out the total force (including gravity) accelerating the weight. Keep in mind that the downward gravity force on M acts as an upward force on m.

Hope this helps.

Regards,
Buzz

 

[jbriggs444]

You have already solved the problem if F ≤ (M+m)g: nothing happens.

Are you sure? Is it possible for the result to be that one weight only lifts off the floor? Can that happen for F ≤ (M+m)g? Can that happen for F >= (M+m)g

Edit: Consider the implications of the simplifying assumptions. If the string, pulley and hook are frictionless and massless then how does the force on either mass vary depending on the motion of the other mass?

 

[Buzz Bloom]

Are you sure? Is it possible for the result to be that one weight only lifts off the floor? Can that happen for F ≤ (M+m)g? Can that happen for F >= (M+m)g

Hi jbriggs:

Good point. You are right. I missed that possibility. Ir depends on the ratio between M and m. I think that if M < 2m, then it is not possible.

Regards,
Buzz

 

[jbriggs444]

Good point. You are right. I missed that possibility. Ir depends on the ratio between M and m. I think that if M < 2m, then it is not possible.

I am trying to suggest that it is simpler than that. The original poster is on the right track with:

Particularly, it seems that i should consider that the tension in the string is half the applied force. In general, any pulley attached to a ceiling is going to exert double the tension force on the ceiling. Why is that?

That is exactly right. A free body diagram focused on the pulley can verify it. If the mass of the pulley assembly is zero, its momentum must be zero. It can be under no net force.

 

[akshay86]

we have tension=(2Mm)g/M+m,but the acceleration of the system is a=F/(M+m)-g.The system has a psudo force acting in the bodies and
so tension=(2Mm)(g+a)/M+m=2Mmg/(M+m)+(2Mm)F/(M+m)^2-2Mmg/(M+m)=(2Mm)F/(M+m)^2
acceleration of larger body,M=Mg-(2Mm)F/(M+m)^2