havsula
- 22
- 2
Hello
I really struggle with understand how and why bolted jonts actually works:
The following figure copied from http://ocw.mit.edu/courses/mechanic...pring-2009/lecture-notes/MIT2_72s09_lec10.pdf shows a bolted joint:
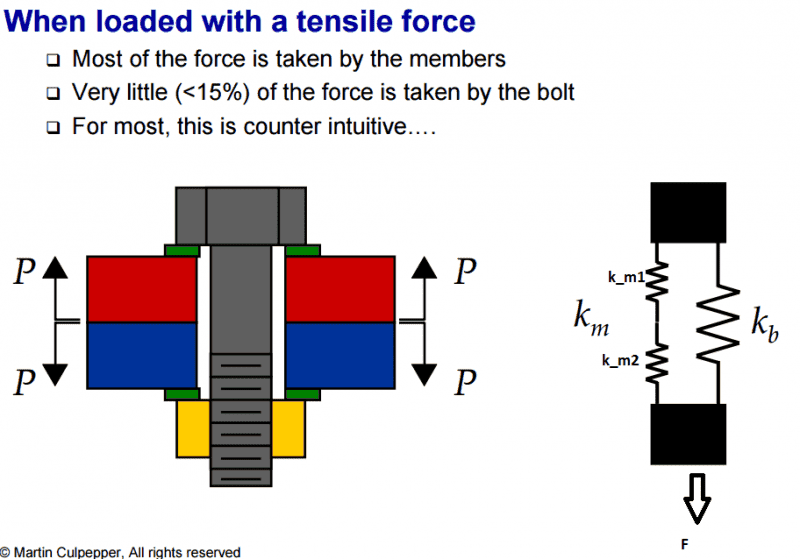
After the bolt is preloaded we have as system where k_m1 and k_m2 are in compression and k_b are streched.
The theory I have founds states that when an externcal force of F is applied to this system, some of the force is taken by the bolt F_b and some of the force are taken by the joints F_a
F = F_b + F_a
But I do not understand how the joints can take up load when they are not connected together. In my head only the bolt can take up force. What do I not understand?
I really struggle with understand how and why bolted jonts actually works:
The following figure copied from http://ocw.mit.edu/courses/mechanic...pring-2009/lecture-notes/MIT2_72s09_lec10.pdf shows a bolted joint:
After the bolt is preloaded we have as system where k_m1 and k_m2 are in compression and k_b are streched.
The theory I have founds states that when an externcal force of F is applied to this system, some of the force is taken by the bolt F_b and some of the force are taken by the joints F_a
F = F_b + F_a
But I do not understand how the joints can take up load when they are not connected together. In my head only the bolt can take up force. What do I not understand?