Understanding CN in Problem Solving: Explained!

[nokia8650]

Problem attached. I can do the question in a variety of ways, however was unable to understand some of the other methods suggested on the markscheme. Please can someone explain them (centre of circle is (r,4), and intersection of line and circle is at (16/5, 12/5).



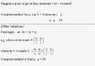
i) ↕CN = 4 sin p + r cos p
Complete method to find r
CN = 4 ; with substituted

r = 2

I do not understand what N is in the above solution, and do not understand how it was done.


The other two solutions are attached.

Thanks!

 

[nokia8650]

Also, i was struggling with the next part, which tells you that the line with eqn. 4x + 3y = q, q>12 is a tangent, and asks one to find q. The markscheme for this part is attached. Could anyone please explain both methods in the markscheme?

Thanks!

 

[rootX]

Do you trying to know why intersection is (16/8,12/5)?

Because, tangents to circle are of equal lengths, one of them is 4, so other also should be of length 4.. now just sqrt(x^2+(3/4x)^2) = 4 ..

and because radius is perp. to y-axis so center is that..

thinking of other questions now..

i) ↕CN = 4 sin p + r cos p
Complete method to find r
CN = 4 ; with substituted

r = 2

I think CN is vertical distance between Center C and x axis.
and p is the angle between the 3/4x line and x-axis and it is equal to the angle between vertical axis through circle center and radius line that touhes 3/4 x line.

once you got that equation, you can plug sinp p and cos p values using the right angle triangle between 3/4x line and x-axistan 2 alpha is using slope method. line perpendicular to y = 3/4x has 4/3 slope = tan 2*alpha..
stopping here <need to do some other work.. will try to come back; interesting question1>
2*alpha is angle between 3/4x line and y axis.. and figure yourself out
why tan alpha = r/yaxis distance(4)

 

[m_s_a]

[url=http://up.x333x.com][PLAIN]http://up.x333x.com/uploads/998eebdc16.jpg[/url][/PLAIN]





very easy
r=2

 

[nokia8650]

Do you trying to know why intersection is (16/8,12/5)?

Because, tangents to circle are of equal lengths, one of them is 4, so other also should be of length 4.. now just sqrt(x^2+(3/4x)^2) = 4 ..

and because radius is perp. to y-axis so center is that..

thinking of other questions now..



I think CN is vertical distance between Center C and x axis.
and p is the angle between the 3/4x line and x-axis and it is equal to the angle between vertical axis through circle center and radius line that touhes 3/4 x line.

once you got that equation, you can plug sinp p and cos p values using the right angle triangle between 3/4x line and x-axis


tan 2 alpha is using slope method. line perpendicular to y = 3/4x has 4/3 slope = tan 2*alpha..
stopping here <need to do some other work.. will try to come back; interesting question1>
2*alpha is angle between 3/4x line and y axis.. and figure yourself out
why tan alpha = r/yaxis distance(4)

Thanks so much for the help! Could you please explain again why tan 2a = 4/3?

Also, does anyone have any ideas for the second part (posted in my second post)?

Thanks