Understanding Complex Planes-Graphs - Get Explanations Here

[Bassalisk]

Hello,

I find those colourful graphs of complex functions very interesting.

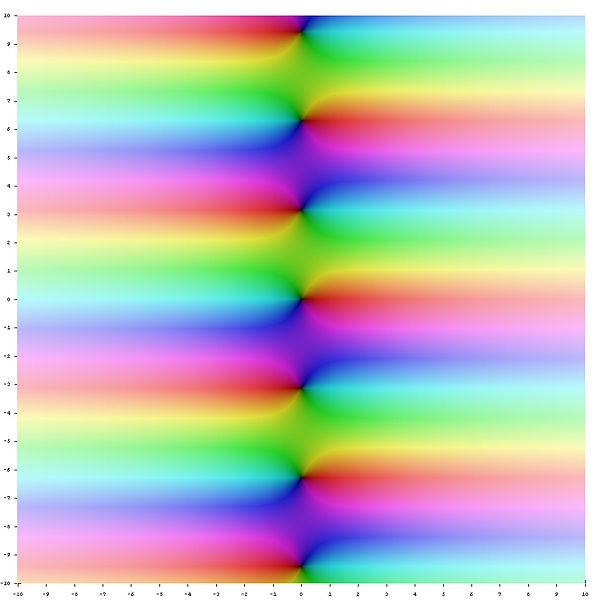
But other than being thrilled by various colours, I have no idea what any of those mean.

Can anybody provide a good source of explanations of these graphs? I would really like to learn how to read them. I don't know what terms do I have to google to get an explanation for this.

 

[mathwonk]

well try to picture a disc wrapping around itself twice, sending th center to the center.

I.e. try to picture the map z-->z^2 in the plane. you take a disc and cut it along a radius. then you wrap it around itself twice and try to glue the edges back together. theydon't quite work since you would have to pass one edge through the other.

but you get something looking like a spiral staircase. if you look at your picture, it is just a bunch of spiral staircases, spiraling at those special points in the middle.

 

[Bassalisk]

well try to picture a disc wrapping around itself twice, sending th center to the center.

I.e. try to picture the map z-->z^2 in the plane. you take a disc and cut it along a radius. then you wrap it around itself twice and try to glue the edges back together. theydon't quite work since you would have to pass one edge through the other.

but you get something looking like a spiral staircase. if you look at your picture, it is just a bunch of spiral staircases, spiraling at those special points in the middle.

Interesting approach. Not going to lie and tell you that I understand you 100%, but I am on the right track.

Thank you.

 

[Studiot]

I don't know what terms do I have to google to get an explanation for this.

Google "winding number" (perhaps choose the images tab - Wiki or Wolfram are quite technical)