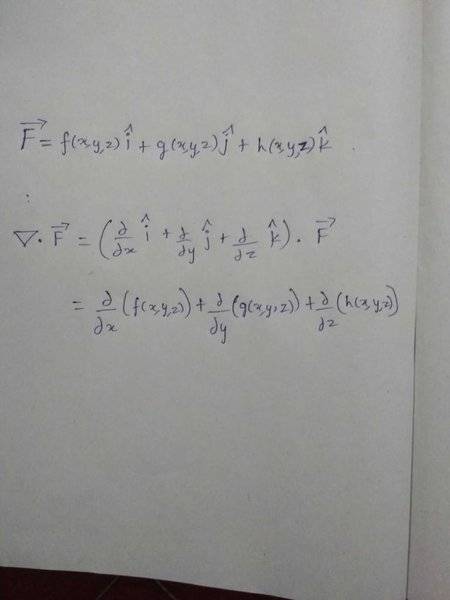Perhaps we can figure that out by taking it into account.
http://mathworld.wolfram.com/Divergence.html takes the approach used in physics:
From the viewpoint of doing rigorous mathematics, making that definition precise would require some work!
Wolfram's abbreviated derivation of the divergence in Cartesian coordinates is:
To explain that proof at the level of a physics textbook, we can consider the cube to be small enough that the components of the vector field within are sufficiently approximated by linear functions.
For example, for the x-component of ##\overrightarrow{F}##, we assume:
## F_x( x_0 + x, y_0 + y, z_0 + z ) = F_x(x_0,y_0,z_0) + \frac{\partial F_x}{\partial x}| _{p_0} x + \frac{\partial F_x}{\partial y}|_{p_0}y + \frac{\partial F_x}{\partial z}|_{p_0} z ##.
where ##p_0 = (x_0,y_0,z_0)## is the point where we wish to compute the divergence of ##F##
For simplicity of notation, I will abbreviate that as
##F_x = F_{x_0} + Ax + By + Cz##
We compute the flux through a cube with sides ##\triangle s## centered on ##(x_0,y_0,z_0)## with edges parallel to the coordinate axes.
Consider computing the flux through the two faces of the cube that lie in the y-z plane. This involves using the unit normal vectors to those faces, which are (-1,0,0) and (1,0.0). For the face with normal (-1,0,0) the integration is
##\int_{y_0 -\triangle s/2}^{y_0 + \triangle s/2} \int_{z_0 - \triangle s/2}^{z_0 + \triangle s/2} (-1) ( F_{x_0} +A(- \triangle s/2) + B y + Cz)\ dz dy ##
## = \int_{y0 - \triangle s/2}^{y_0 + \triangle s/2} ( -F_{x_0} \triangle s + A (\triangle s/2) (\triangle s) - B y \triangle s - C (\big{|}_{z_0 - \triangle s/2}^ {z_0 + \triangle s/2} z^2/2) \ dy ##
## = \int_{y0 - \triangle s/2}^{y_0 + \triangle s/2} ( -F_{x_0} \triangle s + A (\triangle s/2) (\triangle s) - B y \triangle s - C 2 z_0 \triangle s/2) dy ##
## = (- F_{x_0}\triangle s) \triangle s + (A(\triangle s/2)(\triangle s))\triangle s - (B \triangle s) (2y_0 \triangle s)/2 - (C 2 z_0 \triangle s/2)(\triangle s) #### = -F_{x0} \triangle s^2 + A \triangle s^3/2 - By_0 \triangle s^2 - C z_0 \triangle s^2 ##
For the face with normal (1,0,0), the integration is
##\int_{y_0 -\triangle s/2}^{y_0 + \triangle s/2} \int_{z_0 - \triangle s/2}^{z_0 + \triangle s/2} (1) ( F_{x0} + A \triangle s/2 + B y + Cz)\ dz dy ##
## = F_{x0} \triangle s^2 + A \triangle s^3/2 + By_0 \triangle s^2+ C z_0 \triangle s^2 ##
Adding the results for the two faces, the total flux in the x-direction is
## 2 A \triangle s^3/2 = A \triangle s^3 = \frac{\partial F_x}{\partial x} | _{p_0} \triangle s^3##.
By similar calculations for the flux in the y and z direction the total flux through the cube is:
##\frac{\partial F_x}{\partial x} | _{p_0} \triangle s^3 + \frac{\partial F_y}{\partial y}|_{p_0} \triangle s^3 + \frac{\partial F_z}{\partial z}|_{p_0} \triangle s^3 ##
To obtain the divergence, we divide the total flux by the volume ##\triangle s^3## of the cube, so
## Div\ F(x,y,z)| _{(x_0,y_0,z_0)} =
\frac{\partial F_x}{\partial x} | _{p_0} + \frac{\partial F_y}{\partial y}|_{p_0} + \frac{\partial F_z}{\partial z}|_{p_0} ##