- #1
tomtomtom1
- 160
- 8
- Homework Statement
- Understanding the Force / Pressure Equation along a wall and across a surface area
- Relevant Equations
- p = density * gravity * Distance from the water surface.
Hello all
I am trying to understand the pressure equation.
I have the following question:-
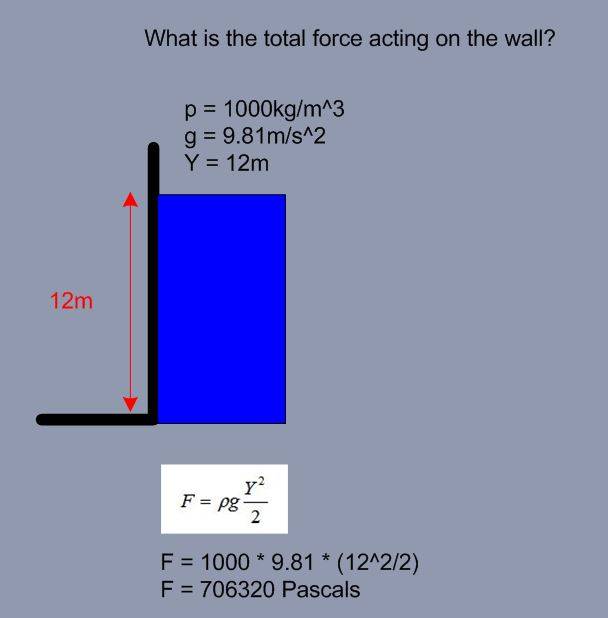 I understand this, to me what this says to me is the total force acting on the wall as a result of the water of 12m is 706320 Pascals.This is where I get a little confused, I have the following question:-
I understand this, to me what this says to me is the total force acting on the wall as a result of the water of 12m is 706320 Pascals.This is where I get a little confused, I have the following question:-
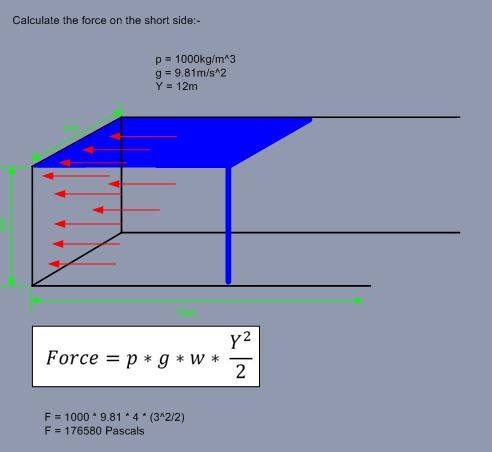
Now I am asked to calculate the total force on a surface area of a wall and because of this I have been told to use a difference equation which involves w i.e. the width.
Am I correct in thinking that the reason why the equations are different is because the first question is only asking me to find the total force in 1 dimension whereas the second question I am asked to find the force across an area which is in 2 dimensions
Is this correct?
Thank you.
I am trying to understand the pressure equation.
I have the following question:-
Now I am asked to calculate the total force on a surface area of a wall and because of this I have been told to use a difference equation which involves w i.e. the width.
Am I correct in thinking that the reason why the equations are different is because the first question is only asking me to find the total force in 1 dimension whereas the second question I am asked to find the force across an area which is in 2 dimensions
Is this correct?
Thank you.