xzibition8612 said:
Homework Statement
See attachment.
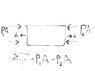
The net pressure force on this control volume is P1*A - P2*A. My question concerns the direction signs.
My thinking is this:
The unit vector on the control volume naturally points outward (n hat). Since the pressure force PA is pushing TOWARDS the control volume, dotting PA and (n hat) would give you -PAn (since the force and unit vector are in opposite directions). Summing the pressure force on this control volume should then yield -P1A-P2A. So I'm very confused why the correct answer is P1A-P2A. Thanks. Maybe I screwed up on the unit vector, is it different for pressure?
Homework Equations
The Attempt at a Solution
This is a very good question. The pressure is part of the stress tensor which can be expressed, for negligible viscous situations, as
[tex]\vec{σ}=-P(\vec{i_x}\vec{i_x}+\vec{i_y}\vec{i_y}+\vec{i_z}\vec{i_z})[/tex]
The stress vector on a surface bounding a region is obtained by dotting the stress tensor with an outwardly directed unit normal [itex]\vec{i_n}[/itex]. The stress vector on the surface is the force per unit area exerted
by the material in the region toward which the normal is pointing, and
on the material from which the normal is pointing.
For your problem, the outwardly directed unit normal for the boundary on the right is given by [itex]\vec{i_n}=+\vec{i_x}[/itex]. So, if you dot the stress tensor with this unit normal, you get a stress vector on the right boundary of [itex]-P\vec{i_x}[/itex]. For the boundary on the left, the outwardly directed unit normal is [itex]\vec{i_n}=-\vec{i_x}[/itex]. So, if you dot the stress tensor with this unit normal, you get a stress vector on the left boundary of [itex]+P\vec{i_x}[/itex].
I hope this helps. It is important to recognize that the pressure is part of the stress tensor, and also to make use of the Cauchy stress relationship which says that the stress vector on a surface is equal to the stress tensor dotted with a unit normal to the surface. It also helps to know dyadic notation, which makes it easy to dot second order tensors with vectors.
