Understanding Tension Force: A Beginner's Guide to Physics

[jamiebean]

Homework Statement

A block of mass is suspended from the ceiling by a string as shown in the figure below. Two forces F1 and F2 cause the string to bend as shown in the figure. The section AB of the string makes an angle of α=43.5 degree with the horizontal line. The mass of the block is m=46.9kg. What is the tension of section AB of the string? g=9.8ms-2 The answer should be in unit of N.

Relevant Equations

f=ma

I am new to physics

I have no idea how the forces work and how to calculate the tension with f=ma
thank you very much..

 

[Gaussian97]

First of all, what is the acceleration of the system?

 

[Merlin3189]

If you understand resolving forces in different directions or finding the horizontal and vertical component of a force, that will help.
Then you can consider the forces at A or B and look just at the vertical or just at the horizontal forces.

 

[haruspex]

I am new to physics
I have no idea how the forces work and how to calculate the tension with f=ma
thank you very much..

Have you been taught to draw free body diagrams? Draw one for point B. Consider the balance of forces.

 

[Lnewqban]

I am new to physics
I have no idea how the forces work and how to calculate the tension with f=ma

How new and to what level?
Without the bend of the string ($F_1=0$ and $F_2=0$), could you solve the problem?

 

[jamiebean]

First of all, what is the acceleration of the system?

is it g=9.8 ?

 

[jamiebean]

How new and to what level?
Without the bend of the string ($F_1=0$ and $F_2=0$), could you solve the problem?

u could assume that I know nothing about forces haha

 

[jamiebean]

Have you been taught to draw free body diagrams? Draw one for point B. Consider the balance of forces.

like this?

 

[jamiebean]

How new and to what level?
Without the bend of the string ($F_1=0$ and $F_2=0$), could you solve the problem?

Ft=46.9kg x 9.8 + 46.9x0
=459.62N

?

 

[Gaussian97]

is it g=9.8 ?

So the system is falling in free fall?

 

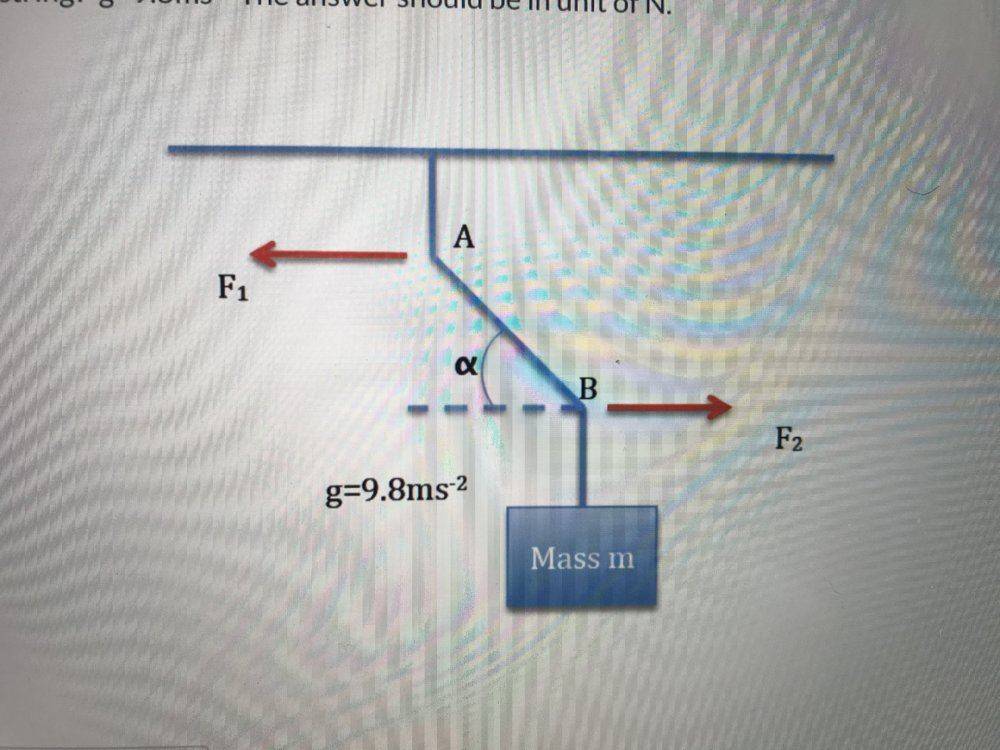
[jamiebean]

So the system is falling in free fall?

oh! the acceleration should be 0

 

[haruspex]

like this?View attachment 258132

Right, so what equations do you get for the balance of forces acting at B? Which of them gives you the tension?

 

[jamiebean]

Right, so what equations do you get for the balance of forces acting at B? Which of them gives you the tension?

how can I calculate forces of f1 and f2? And how can I balance the forces?

 

[haruspex]

how can I calculate forces of f1 and f2? And how can I balance the forces?

We are only looking at forces acting at B, so F1 is not relevant.
There are, in principle, two directions to consider at B. You can choise any two, but here it will be simplest to consider horizontal and vertical. You can write an equation (∑F=ma) for each, though you might not need both.

In these questions you seem to be confused about what a means in F=ma. It means the acceleration which is happening; if the system is static the acceleration is zero.

 

[jamiebean]

We are only looking at forces acting at B, so F1 is not relevant.
There are, in principle, two directions to consider at B. You can choise any two, but here it will be simplest to consider horizontal and vertical. You can write an equation (∑F=ma) for each, though you might not need both.

In these questions you seem to be confused about what a means in F=ma. It means the acceleration which is happening; if the system is static the acceleration is zero.

so ,does F2=0?

 

[jamiebean]

We are only looking at forces acting at B, so F1 is not relevant.
There are, in principle, two directions to consider at B. You can choise any two, but here it will be simplest to consider horizontal and vertical. You can write an equation (∑F=ma) for each, though you might not need both.

In these questions you seem to be confused about what a means in F=ma. It means the acceleration which is happening; if the system is static the acceleration is zero.

then how can I calculate the tension of ab?
sorry for my stupid questions..

 

[jamiebean]

then how can I calculate the tension of ab?
sorry for my stupid questions..

We are only looking at forces acting at B, so F1 is not relevant.
There are, in principle, two directions to consider at B. You can choise any two, but here it will be simplest to consider horizontal and vertical. You can write an equation (∑F=ma) for each, though you might not need both.

In these questions you seem to be confused about what a means in F=ma. It means the acceleration which is happening; if the system is static the acceleration is zero.

is the answer 667.7082?
I first calculated the tension of the weight: 46.9x9.8=459.6
then I used 459.6/sin43.5to calculate the tension of ab

is this correct?

 

[haruspex]

is the answer 667.7082?
I first calculated the tension of the weight: 46.9x9.8=459.6
then I used 459.6/sin43.5to calculate the tension of ab

is this correct?

Looks right. But where the answer is the result of multiplying and dividing a bunch of inputs, you should not quote more significant figures in the answer than in the input number with the fewest. So 668N is a better answer,

 

[Merlin3189]

I first calculated the tension of the weight: 46.9x9.8=459.6
then I used 459.6/sin43.5to calculate the tension of ab

So you looked at point B and considered just the vertical forces

getting W=T sin 43.5
Once you know the tension, if you consider only horizontal forces you get your result for F2.

Why do you not need a calculation to find F1 ?

 

[haruspex]

So you looked at point B and considered just the vertical forces
View attachment 258135getting W=T sin 43.5
Once you know the tension, if you consider only horizontal forces you get your result for F2.

Why do you not need a calculation to find F1 ?

The question does not ask for F1 and F2.

 

[Merlin3189]

I was just mentioning it as a rider. It is a trivial addition, but might help understanding of the situation.

 

[Lnewqban]

u could assume that I know nothing about forces haha

Time to learn, then.

You have to deal with two types of forces: the real thing (your hand holding a bucket of water) and the imaginary thing (the abstract representation; hence, the confusing vectors that you are studying).

* The real thing in our particular problem:
A block of mass is suspended from the ceiling by a string.

Gravity pulls all objects down with the same acceleration (please, don't ask me why).
That means that, in ideal abstract conditions of no air friction, drag or resistance, the speed of all free-falling objects will increase at a rate of 9.81 m/s per each second $(g=9.81~m/s^2)$.

The string of our problem is avoiding the free fall and subsequent acceleration of the block.
We must have a force that opposes the force of gravity, having exactly the same magnitude of the weight of our block and pointing straight up (opposite direction).
Newton explained that the pulling force (in Newtons) of the string over the block is always proportional to its mass (in Kg).
$g=F/m$

Copied from
https://en.wikipedia.org/wiki/Force

"In physics, a force is any interaction that, when unopposed, will change the motion of an object. A force can cause an object with mass to change its velocity (which includes to begin moving from a state of rest), i.e., to accelerate. Force can also be described intuitively as a push or a pull. A force has both magnitude and direction, making it a vector quantity. It is measured in the SI unit of Newtons and represented by the symbol F.

The original form of Newton's second law states that the net force acting upon an object is equal to the rate at which its momentum changes with time. If the mass of the object is constant, this law implies that the acceleration of an object is directly proportional to the net force acting on the object, is in the direction of the net force, and is inversely proportional to the mass of the object."

* The imaginary thing in our particular problem:
A block of mass is acted upon by a vertical F vector from the ceiling and by the vertical mg vector from the ground. The net effect of both vectors is zero; hence, the block does not move (its velocity is zero, while its potential acceleration (if released) would be g).

Because of that, you need to become proficient in addition of vectors (which frequently form triangles) and trigonometry (to solve angles and sides of those triangles).
Please, see:
http://hyperphysics.phy-astr.gsu.edu/hbase/vect.html#veccon