Wetting on the outside of a glass cylinder

[guv]

Homework Statement

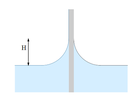
As in the figure, when water wets on the outside of the glass cylinder, it follows a shape as shown. Is it possible to derive or estimate how $H$ depends on $g$, water density $\rho$, radius of the glass tube $r_0$, surface tension $\sigma$, wetting angle $\theta$ at the top?

Relevant Equations

$F_{surface \; tension} = \int_0^H \pi (r(y)^2 - r_0^2) \rho g dy$

There are two difficulties, first $r(y)$ is not known, the surface tension force $F_{surface \; tension}$ is not known either. We can write net surface tension force as
$F_{surface \; tension} = \int_0^H 2 \pi r (\sin \arctan \frac{dy}{dr(y)}) dy$

Is there something else we could use to analyze the shape of the water surface $r(y)$?

A related question as I am thinking about this is how to apply minimization of potential energy? Maybe variational principle could yield the ideal curve $r(y)$? This then reminds me how we generally approach wetting inside of a glass tube, there we simply use a force balance and I don't see how we could use energy minimization principle for the internal wetting setup.

Looking for ideas how you might approach this, thanks!

 

[Chestermiller]

Do you know how to solve this for meniscus on a flat plate?

For the cylindrical problem, I would arc length s measured downward from the top as the independent variable and the contact angle $\phi(s)$ as the dependent variable. Then $$\frac{dz}{ds}=\cos{\phi}$$and $$\frac{dr}{ds}=\sin{\phi}$$where z is measured downward from the contact point.

There are going to be differential equations with respect to s.

 

[haruspex]

The force on the LHS of your equation appears to be the vertical component only.
Can you rewrite it in terms of $\sigma$ and $r'$, and, instead of an integral, just address the element between $r$ and $r+dr$?

 

[guv]

Thanks for the ideas, I wasn't sure if I needed to consider Young's equation and the multi-phase interactions to come up with an reasonable estimation. It looks like people are still (in 2022) trying to work out the meniscus for the water surface inside a cylindrical tube. So this is not a trivial problem. However, maybe as an extremely rough estimation, from the equations above, we can say the weight of the fluid is $\propto H^3 \rho g$, while the surface tension force is $\propto 2 \pi r_0 \cos \theta$, therefore
$H \propto \sqrt[3]{ \frac{ \sigma r_0}{\rho g} }$

The problem with this estimation I can see is proportionality on $r_0$, capillarity suggests the smaller the $r_0$, the greater the $H$.

Anyways, I will need to think about this more thoroughly. Again thanks for the suggestions.

 

[Chestermiller]

Thanks for the ideas, I wasn't sure if I needed to consider Young's equation and the multi-phase interactions to come up with an reasonable estimation.

This would definitely be the approach that I would use. If you would like me to flesh out the analysis, please let me know. My current assessment is that it will involve be a 2nd order ODE, split boundary value problem solving the the liquid reduced pressure value at the contact location.

 

[guv]

This would definitely be the approach that I would use. If you would like me to flesh out the analysis, please let me know. My current assessment is that it will involve be a 2nd order ODE, split boundary value problem solving the the liquid reduced pressure value at the contact location.

Definitely would be interested to see how you might approach this with more details. Thanks!

 

[Chestermiller]

Definitely would be interested to see how you might approach this with more details. Thanks!

OK. The unit vector in the s direction is $$\hat{i}_s=\cos{\phi}\hat{i}_z+\sin{\phi}\hat{i}_r$$If we do a differential force balance for the "window" of interface between s and $s+ds$ and between $\theta$ and $\theta+d\theta$, we obtain $$\sigma\frac{\partial (r\hat{i}_s)}{\partial s}ds d\theta+\sigma\frac{\partial \hat{i}_\theta}{\partial \theta}ds d\theta+(p_a-p_l)rd\theta ds(-\hat{i}_n)=0$$or$$\sigma\frac{\partial (r\hat{i}_s)}{\partial s}-\sigma\hat{i}_r=(p_a-p_l)r\hat{i}_n\tag{1}$$where $p_l$ is the pressure on the liquid side of the interface: $$p_l=p_a-\rho g(h-z)\tag{2}$$with h representing the (unknown) height of the contact point above the pool surface. The unit vector $\hat{i}_n$ is the unit normal vector directed from the water side of the interface to the air side of the interface, and $\sigma$ is the surface tension.$$\hat{i}_n=\cos{\phi}\hat{i}_r-\sin{\phi}\hat{i}_z$$If we combine Eqns. 1 and 2, and dot the resulting relationship with $\hat{i}_n$, we obtain $$\sigma \frac{d\phi}{ds}-\sigma \frac{\cos{\phi}}{r}=\rho g (h-z)$$This is the Young equation in terms of our parameters.

OK so far?

 

[guv]

OK. The unit vector in the s direction is $$\hat{i}_s=\cos{\phi}\hat{i}_z+\sin{\phi}\hat{i}_r$$If we do a differential force balance for the "window" of interface between s and $s+ds$ and between $\theta$ and $\theta+d\theta$, we obtain $$\sigma\frac{\partial (r\hat{i}_s)}{\partial s}ds d\theta+\sigma\frac{\partial \hat{i}_\theta}{\partial \theta}ds d\theta+(p_a-p_l)rd\theta ds(-\hat{i}_n)=0$$or$$\sigma\frac{\partial (r\hat{i}_s)}{\partial s}-\sigma\hat{i}_r=(p_a-p_l)r\hat{i}_n\tag{1}$$where $p_l$ is the pressure on the liquid side of the interface: $$p_l=p_a-\rho g(h-z)\tag{2}$$with h representing the (unknown) height of the contact point above the pool surface. The unit vector $\hat{i}_n$ is the unit normal vector directed from the water side of the interface to the air side of the interface, and $\sigma$ is the surface tension.$$\hat{i}_n=\cos{\phi}\hat{i}_r-\sin{\phi}\hat{i}_z$$If we combine Eqns. 1 and 2, and dot the resulting relationship with $\hat{i}_n$, we obtain $$\sigma \frac{d\phi}{ds}-\sigma \frac{\cos{\phi}}{r}=\rho g (h-z)$$This is the Young equation in terms of our parameters.

OK so far?

I agree with the final equation being the Young's equation in this setup, can you elaborate on how this part $\sigma\frac{\partial (r\hat{i}_s)}{\partial s}ds d\theta+\sigma\frac{\partial \hat{i}_\theta}{\partial \theta}ds d\theta$ is obtained. They are correct, I am wondering if these come from any formal definition such as $\nabla \cdot \hat n$, in particular, $\frac{\partial (r\hat{i}_s)}{\partial s}ds d\theta$ and $\frac{\partial \hat{i}_\theta}{\partial \theta}ds d\theta$

 

[Chestermiller]

I agree with the final equation being the Young's equation in this setup, can you elaborate on how this part $\sigma\frac{\partial (r\hat{i}_s)}{\partial s}ds d\theta+\sigma\frac{\partial \hat{i}_\theta}{\partial \theta}ds d\theta$ is obtained. They are correct, I am wondering if these come from any formal definition such as $\nabla \cdot \hat n$, in particular, $\frac{\partial (r\hat{i}_s)}{\partial s}ds d\theta$ and $\frac{\partial \hat{i}_\theta}{\partial \theta}ds d\theta$

The in-plane force on the side of our little window at $s+ds$ is $$[\sigma(rd\theta)\hat{i}_s]_{s+ds}$$The in-plane force on the side of our little window at $s$ is $$[\sigma(rd\theta)\hat{i}_s]_{s}$$The in-plane force on the side of our little window at $\theta +d\theta$ is $$[\sigma ds\hat{i}_{\theta}]_{\theta +d\theta}$$The in-plane force on the side of our little window at $\theta$ is $$[\sigma ds\hat{i}_{\theta}]_{\theta}$$The pressure force normal to the window is $$(p_a-p_l)(rd\theta)ds(-\hat{i}_n)$$
What does this give for the force balance on the window?

 

[guv]

Thanks for the clarification. What would you suggest how to determine $h$ from here? It looks like we need boundary condition for $\phi(z=0)$ which needs to be determined from Young's equation at the air-glass-water contact point? The other boundary condition $r(z=0) = r_0$ is given. i.e. if we are given $r_0, \phi(z=0)$, then $h$ should be uniquely determined including $s(\phi)$. Alternatively, one can also start with $r_0$ and the surface energy numbers of air-glass-water to determine $\phi(z=0)$ and subsequently the other parameters.

 

[Chestermiller]

Thanks for the clarification. What would you suggest how to determine $h$ from here? It looks like we need boundary condition for $\phi(z=0)$ which needs to be determined from Young's equation at the air-glass-water contact point? The other boundary condition $r(z=0) = r_0$ is given. i.e. if we are given $r_0, \phi(z=0)$, then $h$ should be uniquely determined including $s(\phi)$. Alternatively, one can also start with $r_0$ and the surface energy numbers of air-glass-water to determine $\phi(z=0)$ and subsequently the other parameters.

The next step is to reduce the equations to dimensionless form. For all length parameters (including radius), I would use the characteristic length scale $\sqrt{\frac{\sigma}{\rho g}}$.

In terms of the dimensionless parameters, at s = 0, $\phi$ is equal to the contact angle $\phi_0$ (specified), and at infinite s, $\phi=\frac{\pi}{2}$. The dimensionless h has to be chosen so that, at large s (say s = 10), z =h and $\phi=\frac{\pi}{2}$. In this split boundary value problem, you would iterate on h until these conditions at the far end are satisfied.

I would start out first solving the problem with no curvature, where the curvature $\cos{\phi}/r$ approaches zero. Then I would use the h value for this case as a starting guess for the problem for a curved rod.

 

[guv]

Interesting... My first thought was using matlab ode solver but I can see where your approach is coming from. Thanks!

 

[Chestermiller]

Interesting... My first thought was using matlab ode solver but I can see where your approach is coming from. Thanks!

You can still use the matlab equation solver on your 3 1st order odes