Understanding the electric force felt by the charges on a sphere

[zenterix]

Homework Statement

I am trying to understand another non-trivial derivation and result in Purcell's Electricity and Magnetism.

Consider a charged spherical shell. Charge is distributed over its surface with uniform density $\sigma$.

What is the electrical force experienced by the actual charges that make up the charge distribution?

Relevant Equations

Just inside the shell, the electric field is zero.

Just outside the shell, it is $\frac{\sigma}{\epsilon_0}$.

Consider a small element of charge $dq$ distributed on a small patch of area $dA$.

$$dq=\sigma dA$$

The force on the patch due to the charges in the patch is zero, because when we consider the patch as a system, all the electric forces between the charges contained in it are internal forces that cancel each other out by Newton's third law.

The force experienced by the small patch is due to all the other charges on the spherical shell.

$$d\vec{F} = \vec{E}dq=\vec{E}\sigma dA$$

where $d\vec{F}$ is the force on the patch of charge $dq$.

We don't know what $\vec{E}$ is at this point: is its magnitude zero like the inside of the shell, is it $\frac{\sigma}{\epsilon}$ like right outside the shell? We don't know, but as we see below it will turn out to be an average of these two values.

A thin shell in reality doesn't have zero thickness. Consider the image below, showing a cross-section of a small portion of the shell:

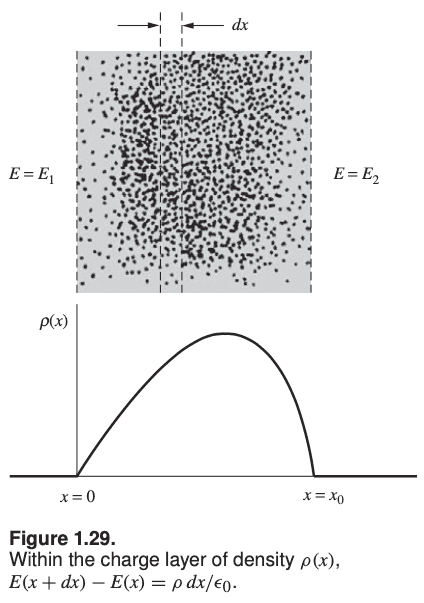
Here we are considering a more general case in which we have electric fields of magnitude $E_1$ and $E_2$ on each side of the shell.

Gauss's Law

$$\vec{E}_2\hat{n}A + \vec{E}_1(-\hat{n})A = \frac{\sigma A}{\epsilon_0}$$

$$\implies \vec{E}_2-\vec{E}_1=\frac{\sigma}{\epsilon_0}\hat{n}$$

$$\implies E_2-E_1=\frac{\sigma}{\epsilon_0}\tag{1}$$

In the latter equation, $E_1$ and $E_2$ are the components in the $x$ direction.

Assume there is a volume charge density $\rho(x)$ extending from $x=0$ to $x=x_0$. Consider a very thin slab of thickness $dx<<x_o$, ie a very thin slice of the cross section of the shell.

The charge per unit area of the slab is $\rho dx$. If the area of the slab is A (where A is an area that visually would be perpendicular to this screen), the total charge in the slab is

$$dq=\rho dx A$$

the force on the slab is then

$$dF = Edq = E\rho dx A$$

* this comment isn't in Purcell, but I understand that $E$ in the equation above is actually $E(x)$.

the total force on the entire shell is $\int dF$

and the total force per unit area on the shell is

$$\frac{F}{A}=\int \frac{dF}{A}=\int_0^{x_0} E \rho dx$$

But we know what $\rho dx$ is because we can apply Gauss's law to the slab. If we take $(1)$ and apply it to the slab we get

$$dE = \frac{\sigma_{slab}}{\epsilon_0}=\frac{\rho dx}{\epsilon_0}$$

$$\implies \rho dx = dE \epsilon_0$$

$$\implies \frac{F}{A}= \int_{E_1}^{E_2} E\epsilon_0 dE = \frac{\epsilon_0}{2}(E_2^2-E_1^1)=\frac{\epsilon_0}{2}(E_2+E_1)(E_2-E_1)$$

However, can we actually use Gauss's law on the slab like this? After all the slab has a thickness dx with charge inside.

But previously above we saw from Gauss's law that

$$E_2-E_1=\frac{\sigma}{\epsilon_0}$$

$$\implies \frac{F}{A}=\frac{E_1+E_2}{2}\sigma$$

This result means that the force per unit area on the charge layer is determined by the mean of the external field on one side and that on the other.

Now a few questions about this:

- This result is independent of the thickness of the layer, as long as it is small relative to the total area. How do we reason about the issue of thickness of the layer? The above derivations treated the thin slab in the shell as if it were a thin sheet, inside of a medium (the shell cross-section) that has varying electric field. The system is the shell cross-section, and we summed up the force due to the electric field over all the components of the cross-section, ie the thin slabs. And... I need to think more here.

- This calculation was done for a cross-section. We derived the result that the force per area on the cross-section is related to the mean of electric field on each side of the shell, times the surface distribution of charge of the shell. But then we modeled the shell as having thickness, so how can it have surface distribution if it is in fact a volume?

 

[TSny]

But we know what $\rho dx$ is because we can apply Gauss's law to the slab. If we take $(1)$ and apply it to the slab we get

$$dE = \frac{\sigma_{slab}}{\epsilon_0}=\frac{\rho dx}{\epsilon_0}$$

$$\implies \rho dx = dE \epsilon_0$$

$$\implies \frac{F}{A}= \int_{E_1}^{E_2} E\epsilon_0 dE = \frac{\epsilon_0}{2}(E_2^2-E_1^1)=\frac{\epsilon_0}{2}(E_2+E_1)(E_2-E_1)$$

However, can we actually use Gauss's law on the slab like this? After all the slab has a thickness dx with charge inside.

I'm not quite sure what the issue is here. Your equation (1) is for a surface of negligible thickness that has a surface charge density $\sigma$. Now we have a slab of thickness $dx$ with a volume charge density $\rho(x)$. If you are bothered by just switching $\sigma$ to $\rho(x)dx$ in equation (1), then forget (1) and apply Gauss' law directly to the slab. Use a pillbox Gaussian surface.

Gauss' law yields

$(E_b - E_a)A = \frac{Q_{enclosed}}{\epsilon_0}$

Note that $E_b - E_a = dE$ and $Q_{enclosed} = \rho(x)Adx$