williamcarter
- 153
- 4
Moved from a technical forum, so homework template missing
Dear PF members.
I am requesting again your help as I keep struggling with the LaPlace transformation.
I have this exercise to do(please see below)
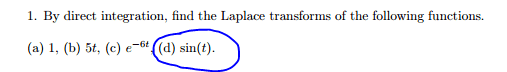
We know that L[f(t)]= integral from 0 to infinity of f(t)*e^(-st) dt
thus in our case, L[f(t)]= integral from 0 to infinity of sin(t)*e^(-st) dt
I tried doing it by parts twice, however I can't reach their answer.Please look below
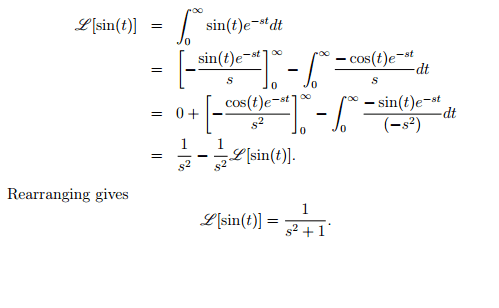
Could you please show me how to solve it?
Thank you in advance.
I am requesting again your help as I keep struggling with the LaPlace transformation.
I have this exercise to do(please see below)
We know that L[f(t)]= integral from 0 to infinity of f(t)*e^(-st) dt
thus in our case, L[f(t)]= integral from 0 to infinity of sin(t)*e^(-st) dt
I tried doing it by parts twice, however I can't reach their answer.Please look below
Could you please show me how to solve it?
Thank you in advance.