PhysicsReaper
- 2
- 0
Hello,
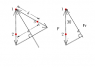
I have the following problem part (b) which I already solved as you can see in the attached image. So I am not asking homework questions, I merely reviewing my homework for a better understanding for the test. I obtained the answer from a friend showing me his method. However, I am studying and a listed solution was the following:
F_y = 2*(k*(q^2/r^2))cos(30)
I've drawn out a force diagram but have no idea how, they have obtained the cosign. In the listed solution they state use oriented the y-axis such that it bisects charges q2 and q3.

I have the following problem part (b) which I already solved as you can see in the attached image. So I am not asking homework questions, I merely reviewing my homework for a better understanding for the test. I obtained the answer from a friend showing me his method. However, I am studying and a listed solution was the following:
F_y = 2*(k*(q^2/r^2))cos(30)
I've drawn out a force diagram but have no idea how, they have obtained the cosign. In the listed solution they state use oriented the y-axis such that it bisects charges q2 and q3.