Confusing diagram of a rotating coil in a magnetic field

[Grizzly_1]

TL;DR Summary

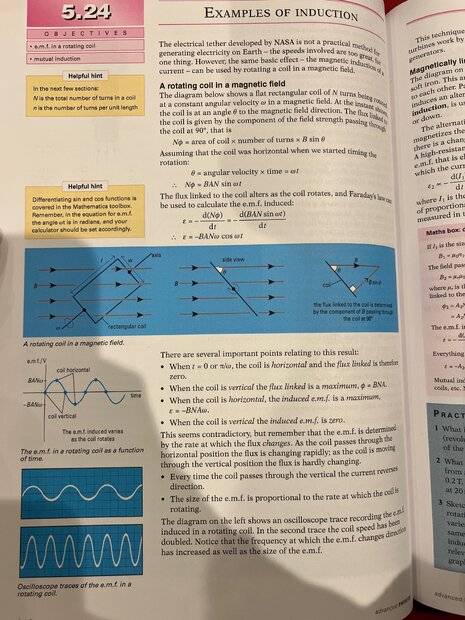
The coil diagram provided seems to contradict itself in the next diagram.

Hello all, I am currently studying for a physics a-level qualification in the UK, I use the AQA specification and I am having trouble understanding this image representing a scenario I found in my textbook. The first image in the three part diagram shows this rotating coil and to me, it makes absolutely no sense how from that image, you arrive at the side view in the second picture (I understand the physics of the side view image). Is this a poorly drawn diagram? or am I missing something? As to me it appears that not only is the coil at an angle to the field but also the axis itself is at an angle to the field, wouldn't this fundamentally change how the magnetic field interacted with it? How can the first image turn into the second if the axis isn't aligned at pi/2 rads to the magnetic field?
Any guidance on this is much appreciated, I am thoroughly confused.

 

[scottdave]

2 ideas about this - either they drew the first one as an isometric drawing to "look" 3d.

or the axis really is at an angle, but when you look at the 2nd drawing, you are looking down the axis, and seeing a cross section of the B lines.

 

[Grizzly_1]

2 ideas about this - either they drew the first one as an isometric drawing to "look" 3d.

or the axis really is at an angle, but when you look at the 2nd drawing, you are looking down the axis, and seeing a cross section of the B lines.

But if the axis really was at an angle, wouldn't this mean that the flux is always hitting at an angle? Surely that means the 2nd drawing is slightly wrong at least.

Thanks for replying!

 

[berkeman]

Is this a poorly drawn diagram?

either they drew the first one as an isometric drawing to "look" 3d.

This^^^

I think the first drawing is a poor representation of the problem, and I would base my calculations on the 2nd drawing.

 

[vanhees71]

Formulae are much more accurate than any picture and sometimes easier to understand. I guess what they mean to depict is that there is a (for simplicity homogeneous) magnetic field, $\vec{B}=B \vec{e}_3$, and a rectangular coil with $N$ windings rotating around a perpendicular axis, say the 1-axis, i.e., it's $\vec{\omega}=\omega \vec{e}_1$. Let's assume the loop is initially oriented such that the rectangle is in the 12-plane. Then the surface-normal vector is given by $\vec{n}=(0,\sin(\omega t),\cos(\omega t)$.

Unfortunately I cannot read the scanned book page well. I guess what they plot is the emf. So let's calculate the emf. from Faraday's Law. It's given by $\mathcal{E}=-\dot{\Phi}$, where $\Phi$ is the flux of the magnetic field through the surface. Let $a$ and $b$ the lengths of the sides of the rectangular $N$-fold loop. Then
$$\Phi=N \vec{B} \cdot a b \vec{n} =a b N B \cos(\omega t) \; \Rightarrow \; \mathcal{E}=-\dot{\Phi}= a b B N \omega \sin(\omega t).$$