zenterix
- 774
- 84
- Homework Statement
- A magnetic dipole is located on the line of symmetry of a bar magnet. What is the work done by an external force to move the dipole a certain distance along this symmetry line?
- Relevant Equations
- I am reading
these notes on magnetic field from MIT OCW's 8.02 course.
There is the following snippet on page 10
At this point it is still not clear to me exactly what a magnetic dipole is. I've done all the calculations for a current-carrying rectangular loop, so I will assume that a magnetic dipole is any current-carrying rectangular loop.
My first question is about the direction of ##\vec{F}_B## in the figure. Why does it point to the left?
The center of mass of the dipole is moving to the right. The magnetic field on the symmetry line points to the right as well. The cross product is zero. Thus, the magnetic force should be zero.
On the symmetric axis of the bar magnet, the magnetic field seems to point in the ##\hat{i}## direction, ie to the right in the figure above.
The rectangular loop has four parts
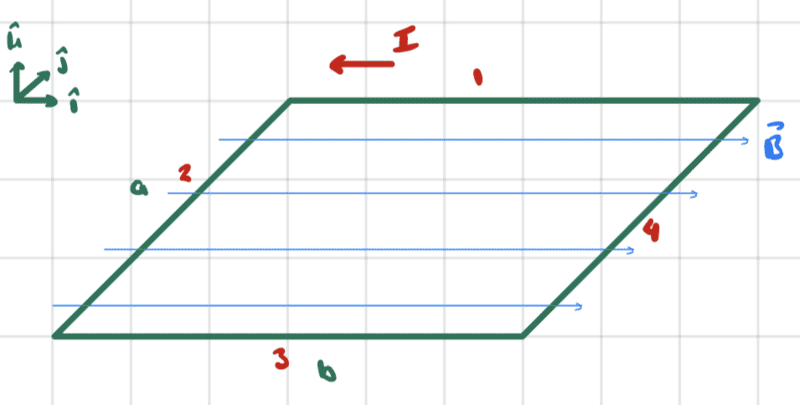
Parts (2) and (4) above are affected by the magnetic field in such a way that a torque is produced.
If the magnetic field were constant (as in the picture above), then torque would be
$$\vec{\tau}=\vec{\mu}\times\vec{B}$$
where ##\mu=I\vec{A}## and ##\vec{A}## is the vector normal to area $A$ of the loop.
The work done by the magnetic field in rotating the dipole by ##d\theta## is
$$dW=(\vec{\tau})_{-\hat{j}}d\theta$$
$$=-(\vec{\mu}\times\vec{B})d\theta$$
and the total work is
$$W=\int_{\theta_i}^{\theta_f} \vec{\mu}\times\vec{B}d\theta$$
$$=\mu B(\cos{\theta_f}-\cos{\theta_i})$$
$$=-\Delta U$$
If we define ##U(\pi/2)=0## then the potential energy function is
$$U(\theta)=-\mu B\cos{\theta}=-\vec{u}\cdot \vec{B}$$
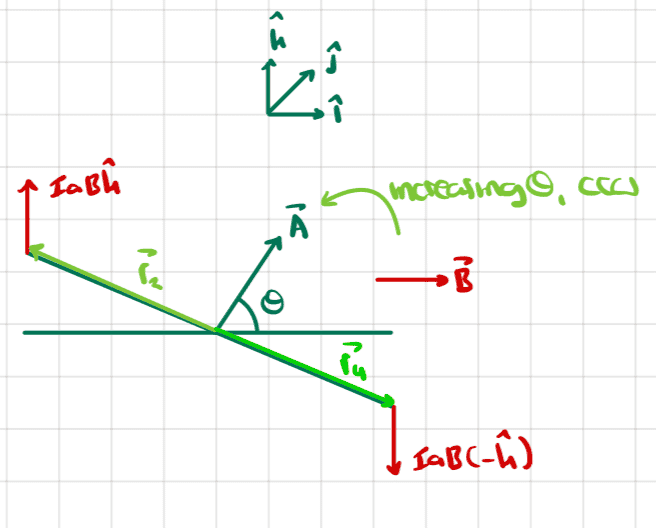
Here is a side view of the dipole when the normal vector forms an angle ##\theta## with the symmetry line
Now consider the situation in the initial figure. The magnetic field is weaker at (4) than at (3).
The quoted snippet above says the dipole is attracted to the bar magnet. How does this happen? After all, the magnetic force does not point towards that bar magnet.
The amount of force ##F_{ext}## exerted by an external agent to move the dipole by a distance ##\Delta x## away from the magnet is, according to the notes
$$F_{ext}\Delta x=W_{ext}=\Delta U=(-\vec{\mu}\cdot\vec{B}(x+\Delta x))-(\vec{\mu}\cdot\vec{B}(x))$$
$$=(-\mu B(x+\Delta x)-(-\mu B(x))$$
$$=-\mu B(x+\Delta x)+\mu B(x)$$
$$=-\mu [B(x+\Delta x)-B(x)]$$
So
$$F_{ext}=-\mu\frac{B(x+\Delta x)-B(x)}{\Delta x}$$
In the limit as ##\Delta x\to 0## we get
$$F_{ext}=-\mu\frac{dB}{dx}$$
which is positive since ##\frac{dB}{dx}<0##.
In these equations, we simply calculated the difference in the potential energy between two points.
I am quite confused by the calculation above.
It is clear to me in the case of no translational motion what the potential energy function represents.
It is simply the negative of the work done by a constant magnetic field in rotating the dipole from a horizontal position (##\theta=\pi/2##) to a position with angle ##\theta##.
In the case of the scenario in the initial figure, it seems to me there is both rotation and translation.
If there were translation but no rotation, the potential energy (##-\vec{\mu}\cdot\vec{B}##) seems that it would not change (because even though ##\vec{B}## is different between two points on the line, ##\vec{\mu}##, which contains the area vector ##\vec{A}##, is still perpendicular ##\vec{B}##).
This seems to mean that the work to move the dipole between two points would be zero and so would the external force.
If, on the other hand, there is also rotation the ##\mu## also changes.
As far as I can tell, the rotation happens during the translation.
The first ##dW## that occurs is with a strong ##\vec{B}## and the final ##dW## that occurs is with the weakest ##\vec{B}## along the trajectory.
I'm having a hard time justifying why we can compare the potential energy from the two different translational positions.
I also can't see why in the calculations above ##\mu## is not a function of ##\theta## in any way. That is, the notes seem not to care about the rotation aspect of the move from ##x## to ##x+\Delta x##.
There is the following snippet on page 10
As we have shown above, the force experienced by a current-carrying rectangular loop (i.e., a magnetic dipole) placed in a uniform magnetic field is zero. What happens if the magnetic field is non-uniform? In this case, there will be a net force acting on the dipole.
Consider a situation where a small dipole ##\vec{\mu}## is placed along the symmetric axis of a bar magnet, as shown in Figure 8.4.4.
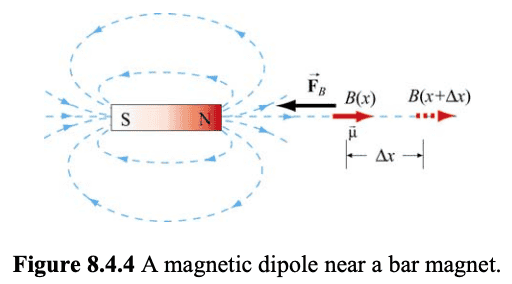
The dipole experiences an attractive force by the bar magnet whose magnetic field is non-uniform in space. Thus, an external force must be applied to move the dipole to the right.
At this point it is still not clear to me exactly what a magnetic dipole is. I've done all the calculations for a current-carrying rectangular loop, so I will assume that a magnetic dipole is any current-carrying rectangular loop.
My first question is about the direction of ##\vec{F}_B## in the figure. Why does it point to the left?
The center of mass of the dipole is moving to the right. The magnetic field on the symmetry line points to the right as well. The cross product is zero. Thus, the magnetic force should be zero.
On the symmetric axis of the bar magnet, the magnetic field seems to point in the ##\hat{i}## direction, ie to the right in the figure above.
The rectangular loop has four parts
Parts (2) and (4) above are affected by the magnetic field in such a way that a torque is produced.
If the magnetic field were constant (as in the picture above), then torque would be
$$\vec{\tau}=\vec{\mu}\times\vec{B}$$
where ##\mu=I\vec{A}## and ##\vec{A}## is the vector normal to area $A$ of the loop.
The work done by the magnetic field in rotating the dipole by ##d\theta## is
$$dW=(\vec{\tau})_{-\hat{j}}d\theta$$
$$=-(\vec{\mu}\times\vec{B})d\theta$$
and the total work is
$$W=\int_{\theta_i}^{\theta_f} \vec{\mu}\times\vec{B}d\theta$$
$$=\mu B(\cos{\theta_f}-\cos{\theta_i})$$
$$=-\Delta U$$
If we define ##U(\pi/2)=0## then the potential energy function is
$$U(\theta)=-\mu B\cos{\theta}=-\vec{u}\cdot \vec{B}$$
Here is a side view of the dipole when the normal vector forms an angle ##\theta## with the symmetry line
Now consider the situation in the initial figure. The magnetic field is weaker at (4) than at (3).
The quoted snippet above says the dipole is attracted to the bar magnet. How does this happen? After all, the magnetic force does not point towards that bar magnet.
The amount of force ##F_{ext}## exerted by an external agent to move the dipole by a distance ##\Delta x## away from the magnet is, according to the notes
$$F_{ext}\Delta x=W_{ext}=\Delta U=(-\vec{\mu}\cdot\vec{B}(x+\Delta x))-(\vec{\mu}\cdot\vec{B}(x))$$
$$=(-\mu B(x+\Delta x)-(-\mu B(x))$$
$$=-\mu B(x+\Delta x)+\mu B(x)$$
$$=-\mu [B(x+\Delta x)-B(x)]$$
So
$$F_{ext}=-\mu\frac{B(x+\Delta x)-B(x)}{\Delta x}$$
In the limit as ##\Delta x\to 0## we get
$$F_{ext}=-\mu\frac{dB}{dx}$$
which is positive since ##\frac{dB}{dx}<0##.
In these equations, we simply calculated the difference in the potential energy between two points.
I am quite confused by the calculation above.
It is clear to me in the case of no translational motion what the potential energy function represents.
It is simply the negative of the work done by a constant magnetic field in rotating the dipole from a horizontal position (##\theta=\pi/2##) to a position with angle ##\theta##.
In the case of the scenario in the initial figure, it seems to me there is both rotation and translation.
If there were translation but no rotation, the potential energy (##-\vec{\mu}\cdot\vec{B}##) seems that it would not change (because even though ##\vec{B}## is different between two points on the line, ##\vec{\mu}##, which contains the area vector ##\vec{A}##, is still perpendicular ##\vec{B}##).
This seems to mean that the work to move the dipole between two points would be zero and so would the external force.
If, on the other hand, there is also rotation the ##\mu## also changes.
As far as I can tell, the rotation happens during the translation.
The first ##dW## that occurs is with a strong ##\vec{B}## and the final ##dW## that occurs is with the weakest ##\vec{B}## along the trajectory.
I'm having a hard time justifying why we can compare the potential energy from the two different translational positions.
I also can't see why in the calculations above ##\mu## is not a function of ##\theta## in any way. That is, the notes seem not to care about the rotation aspect of the move from ##x## to ##x+\Delta x##.
Last edited: