Gryphlet
- 1
- 0
I recently took an exam in my engineering mechanics class and passed the exam except for one question. I have been trying to solve this question after the fact and determine the solution, however neither I nor several engineering tutors have had any success. The professor refuses to give assistance or clarification. Any assistance would be appreciated.
1. Homework Statement
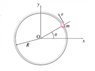
A bead of mass 'm' slides on a rigid circular wire. The coefficient of kinetic friction between the bead and the wire is ## \mu ##. Assume Gravity is negligible.
a. Is speed increasing or decreasing? [correct answer: decreasing]
b. Find an expression for the rate of change of speed. [correct answer: ##\frac {dv} {dt} = \frac {\mu v^2} {r}##]
c. If at t=0 the speed of the bead is ##v_o##, find the speed v(t) as a function of time t. [correct answer: ##v(t) = \frac {r v_o} {r + v_o \mu t}##]
##s = r \theta ##
##v = r \dot \theta ##
##\frac {dv} {dt} = r \ddot \theta ##
##\vec V = r \dot \theta \hat t ##
##\vec a = \frac {v^2} {r} \hat n + \frac {dv} {dt} \hat t ##[/B]
a. The speed of the bead is decreasing due to the presence of friction [correct]
b. Rate of change of speed is equal to ##\frac {dv} {dt}##
Using normal-tangential coordinates, I determined that friction is opposing the direction of motion, in this case the velocity in the tangential direction, thus:
##\sum F_x = -F_f sin \theta ##
##\sum F_y = F_f cos \theta ##[/B]
I am not even sure where to begin with this problem, although I am actively working on it now. The exam is over and I have lost all chance at points but I would still like to understand the concepts behind a problem like this. Any assistance would be appreciated; if there is anything I need to add or change in this problem statement please let me know. Thank you in advance!
1. Homework Statement
A bead of mass 'm' slides on a rigid circular wire. The coefficient of kinetic friction between the bead and the wire is ## \mu ##. Assume Gravity is negligible.
a. Is speed increasing or decreasing? [correct answer: decreasing]
b. Find an expression for the rate of change of speed. [correct answer: ##\frac {dv} {dt} = \frac {\mu v^2} {r}##]
c. If at t=0 the speed of the bead is ##v_o##, find the speed v(t) as a function of time t. [correct answer: ##v(t) = \frac {r v_o} {r + v_o \mu t}##]
Homework Equations
##s = r \theta ##
##v = r \dot \theta ##
##\frac {dv} {dt} = r \ddot \theta ##
##\vec V = r \dot \theta \hat t ##
##\vec a = \frac {v^2} {r} \hat n + \frac {dv} {dt} \hat t ##[/B]
The Attempt at a Solution
a. The speed of the bead is decreasing due to the presence of friction [correct]
b. Rate of change of speed is equal to ##\frac {dv} {dt}##
Using normal-tangential coordinates, I determined that friction is opposing the direction of motion, in this case the velocity in the tangential direction, thus:
##\sum F_x = -F_f sin \theta ##
##\sum F_y = F_f cos \theta ##[/B]
I am not even sure where to begin with this problem, although I am actively working on it now. The exam is over and I have lost all chance at points but I would still like to understand the concepts behind a problem like this. Any assistance would be appreciated; if there is anything I need to add or change in this problem statement please let me know. Thank you in advance!