Upward force due to rotating magnetic field

[Anakratis]

Hey guys,

So I have a bit of an interesting problem to solve here. I'm trying to calculate the upward repulsion force due to eddy currents created in a conductive surface by a rotating magnetic field. I'm doing this for an undergraduate lab project, and want to be able to provide quantifiable results with equations.

Essentially, I'm placing neodymium bar magnets (in a symmetrical fashion, of course) within an acrylic disc that is attached to a basic servo motor and spins extremely fast above a conductive surface like a copper or aluminum plate. This creates a levitation force due to the eddy currents create at such high angular velocities. I'm trying to find a way to actually calculate this upward force due to these eddy currents created.

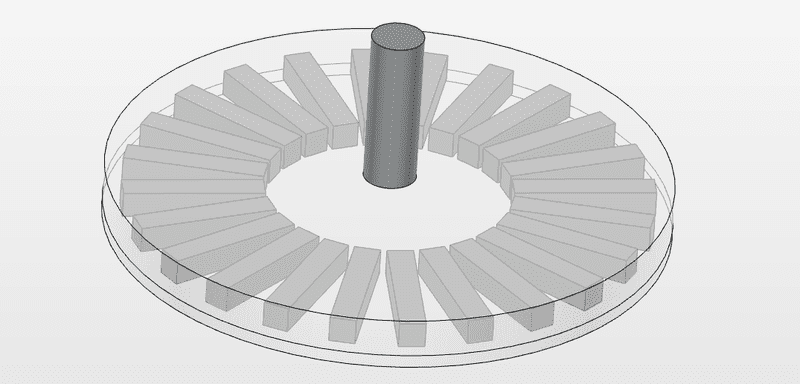
You can look below at the video provided:


I don't even know where to start here, but I do know that we have to somehow use the change in the magnetic field over a conducting surface using a specific linear velocity (which an be converted to RPM). Also using Gauss' law for magnetic field (and the later application of the Lorentz force law):

$$\oint\oint{B\cdot dA} = 0$$

Essentially, I want to be able to input rotations per minute and output the upward force vector, or lift capacity. I realize that this will include many variables, such as the magnetic field strength over the entire surface of the rotor facing the plates. I'm guessing that this is an application of a typical Lorentz force:

$$F = \frac{d\rho}{dt} = q(E + v \times B)$$

Where B is the magnetic field strength, and v is the linear velocity of the spinning rotor moving over a surface relative to the surface - however, I'm getting confused over the direction vectors for B, since shouldn't those differ according to the alignment and placement of the magnets themselves (for example, in which direction would B be if I was using something like a Halbach array)? So the direction of F_B seems a little arbitrary to me.

Any thoughts on where to begin?

 

[Dr. Courtney]

Lots of tricky theory and it may not be possible to solve by first principles without detailed knowledge of the vector fields of the permanent magnets and the conductivity of the materials.

I'd tend to take an empirical approach. With a given weight, the upward force will equal the weight when there is vertical equilibrium. This will allow graphing upward force vs. height for a given set of conditions. Then you can change your conditions to see how the force vs. height curve depends on the conditions.

Eventually some trends will emerge.

 

[Anakratis]

Lots of tricky theory and it may not be possible to solve by first principles without detailed knowledge of the vector fields of the permanent magnets and the conductivity of the materials.

I'd tend to take an empirical approach. With a given weight, the upward force will equal the weight when there is vertical equilibrium. This will allow graphing upward force vs. height for a given set of conditions. Then you can change your conditions to see how the force vs. height curve depends on the conditions.

Eventually some trends will emerge.

Thank you so much for the reply!

I will make sure to conduct the experiment with a wide variety of controls and variables, so I can try to obtain a steady trend for the RPM vs. upward force graph :)

Say that I did actually know the vector fields of the permanent magnets and the conductivity of the material (using AA1370-50 aluminum plates, which has very high conductivity), what else would I need to know before trying to embark on the mathematical journey?

 

[Dr. Courtney]

Thank you so much for the reply!

I will make sure to conduct the experiment with a wide variety of controls and variables, so I can try to obtain a steady trend for the RPM vs. upward force graph :)

Say that I did actually know the vector fields of the permanent magnets and the conductivity of the material (using AA1370-50 aluminum plates, which has very high conductivity), what else would I need to know before trying to embark on the mathematical journey?

It may be amenable to computer modeling, but I doubt pencil and paper solutions are possible.

 

[Anakratis]

It may be amenable to computer modeling, but I doubt pencil and paper solutions are possible.

Hmmmm... So are pencil and paper solutions not possible simply due to the complexity of the magnetic field underneath the rotor (between the rotor and plate)? It seems to me that you can find the net magnitude of eddy currents induced within the plates given a certain magnetic strength and velocity vector (or change in flux), by integration. Then couldn't you something like the Lorentz force law to calculate how the plate is pushing the rotor away? Of course this wouldn't be accurate on pencil and paper, but in theory, is this basically what you would have to do, to create a model for the computer to utilize?

Sorry for constant questions - this is just really interesting to me! :)