Upward force of float moving in an arch under water

[mrapple]

Homework Statement

Curious Question

Relevant Equations

Cos declination angle

a float with 5 pounds of water displacement is resting on the bottom of a pool of water

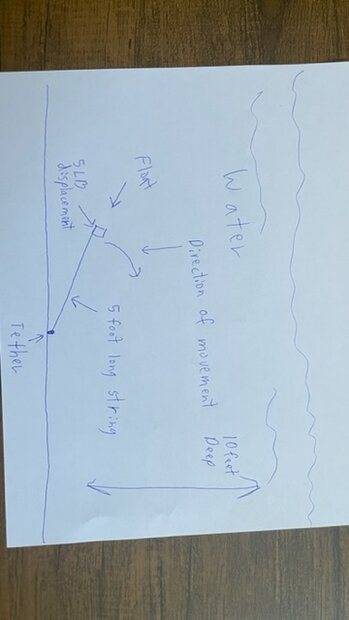10 feet deep. The float is tethered to the bottom of the pool via a string that is pulled tight lengthwise and so is also laying on the bottom of the pool. The string is 4 feet long. If the float is released the float must travel in an arch because of the string tether. What equation do I use to figure out the resulting upward force of the float if it is traveling in an arch?

 

[jbriggs444]

I've clarified via PM that the string is massless and is unaffected by either buoyancy or viscosity. So it remains taut at all times.

It is not clear whether the float is affected by viscosity or, if so, what drag relation we are to assume.

I see no effort, so will refrain from making any suggestions at this time.

 

[mrapple]

(mass)(g)*cos(45)? I have no idea where to start. If you could direct me a little I will try to read up on it on my own. I just need someone to get me started.

 

[mrapple]

Just so I can google the equation. I will do it on my own.

 

[Delta2]

I think this is some sort of reversed pendulum: Instead of the weight of the bob, we have here the buoyancy force minus the weight of the float (which might be negligible) that plays the restorative force and is of course upwards instead of downwards.

 

[jbriggs444]

At any point in the circular arc, you have a net force from buoyancy minus gravity. At 45 degrees above the horizontal, the component of that force along the arc will be (buoyancy - gravity) * cos(45), yes.

However, you are probably better off measuring the angle from the vertical and calling it sin(45) instead. That choice will pay dividends later.

You will wind up with a (nasty) differential equation.

With a simplifying assumption, one could follow the idea offered by @Delta2 and try to treat this as simple harmonic motion.

If we are going to be realistic, there are two additional effects to account for.

1. Water resistance due to viscosity.
2. Water resistance due to inertia.

If we are to make any progress, we should ignore both for now and, perhaps, try to account for them later.

 

[erobz]

Sum the torques about the pivot or if you are considering it a point mass; sum forces in the $\theta$ direction and you will get an equation that describes the motion. Afterwards, you can use that result to find the tension in the string if you sum forces in the $r$ direction.

$$ \sum F_{r} = m \left( \ddot r - r { \dot \theta }^2 \right)$$

$$ \sum F_{\theta} = m \left( r \ddot \theta + 2 \dot r \dot \theta \right)$$

For this particular problem $\dot r = 0, \ddot r = 0$

Is that what you were looking for?

EDIT:
As has been pointed out, the motion of this float would likely be severely dampened from the motion you will solve for using only the forces shown in the diagram.

 

[erobz]

If you sum the torques ( including a quadratic drag force not shown in the diagram )

$$ \circlearrowright^+ \sum \tau = \left( F_b -mg \right) \sin \theta r - \frac{1}{2} \rho A C_D r^3 {\dot \theta}^2 = I \ddot \theta $$

I think that is ok, the drag force will always be aligned with the $\theta$ direction? However, it should only be valid for when $\dot \theta > 0$

At some point it's going to reverse direction and the sign in front of the quadratic drag term flips to positive. How is that usually handled? Is there some way that you can alternate the sign mathematically by using something common like $(-1)^n$?

 

[jbriggs444]

Is there some way that you can alternate the sign mathematically by using something common like $(-1)^n$?

You can stick in something like $\frac{\vec{v}}{|\vec{v}|}$.

But that is just notation. I do not think that it offers any help when trying to solve the differential equation. [And you get the ugly undefinition at v=0]

 

[erobz]

You can stick in something like $\frac{\vec{v}}{|\vec{v}|}$.

But that is just notation. I do not think that it offers any help when trying to solve the differential equation. [And you get the ugly undefinition at v=0]

Yeah, numerically solving for $\dot \theta$ looks straight forward. Its just that you have to watch for the $\dot \theta = 0$ so you can programmatically change the EOM and continue.

I'd expect we'd get this basic behavior (probably more damped though)?

 

[jbriggs444]

I'd expect we'd get this basic behavior (probably more damped though)?

I'd expect to damp fairly quickly from the quadratic regime into a regime where drag is approximately linear. Then one would have a standard overdamped, underdamped or critically damped decay.

 

[erobz]

I'd expect to damp fairly quickly from the quadratic regime into a regime where drag is approximately linear. Then one would have a standard overdamped, underdamped or critically damped decay.

What measure is typically used to delineate the regime change?

 

[jbriggs444]

What measure is typically used to delineate the regime change?

Edit: Maybe the Reynolds number is what you are asking for.

Roughly speaking, I'd say that if the quadratic drag is 10 times the linear drag, then you are in the quadratic regime. If linear drag is 10 times quadratic then you are in the linear regime. In between, you are in a messier regime, having to account for both.

It depends on how accurate you need your predictions to be. You accept the simplifications that will make your calculations easier while still leaving you with an acceptably accurate result.

 

[erobz]

Edit: Maybe the Reynolds number is what you are asking for.

Roughly speaking, I'd say that if the quadratic drag is 10 times the linear drag, then you are in the quadratic regime. If linear drag is 10 times quadratic then you are in the linear regime. In between, you are in a messier regime, having to account for both.

It depends on how accurate you need your predictions to be. You accept the simplifications that will make your calculations easier while still leaving you with an acceptably accurate result.

So, both are working all the time, its just that one dominates the other over say a particular range of Reynolds Numbers? Since the plan of attack is already numerical, changing $F_D$ to :

$$ F_D = \pm \lambda {\dot \theta}^2 -\beta \dot \theta $$

Doesn't really add any more complexity to calculating the solution that I can see ( unless maybe the coefficients $\lambda, \beta$ are strong functions of the Reynolds Number themselves ). What changes can we expect to see in the general behavior of that basic solution curve I presented in doing that? I understand the effect of the stronger damping, what I don't see is the difference in the tail end of the behavior.

 

[jbriggs444]

What changes can we expect to see in the general behavior of that basic solution curve I presented in doing that?

The linearly damped harmonic oscillator is a well studied differential equation that one would encounter in a first semester course on differential equations. It is a linear, homogenous, second order differential equation. For such equations, you get nice analytical solutions in terms of sines, cosines and exponentials. [By contrast, with quadratic drag, the differential equation is no longer "linear"]

Underdamped, you get a sine wave within an exponentially decaying envelope.
Overdamped, you get a decaying exponential (technically, a sum of two)
Critically damped, you get a decaying exponential.

If the characteristic equation (a quadratic in this case) for the differential equation has two real roots, you get overdamping. If the characteristic equation has two complex roots (which will be conjugates), you get underdamping. If the equation has a single, repeated real root, you get critical damping.

In automobile shock absorbers, one normally designs for critical damping. The diagnostic test is to push down on the car's bumper, then release and see whether the car oscillates or smoothly returns to normal with no oscillation. If it bounces up and then back down, that is underdamping. The shocks are worn and need to be replaced. [This worked for the typical shocks that I grew up with -- linear valve strategies. It seems that much more complex strategies are available these days].

I've never looked much at pure quadratic damping. Intuitively, I'd expect that since the drag drops away dramatically near zero velocity that there is no possibility of overdamping, that a small oscillation will always exist and may be long-lived. I'd expect convergence to an ever-more-slowly decaying sine wave.