Verify Sol. of an Dynamic Problem with 2 Wheels

[parmalesso]

1. The problem is the following:

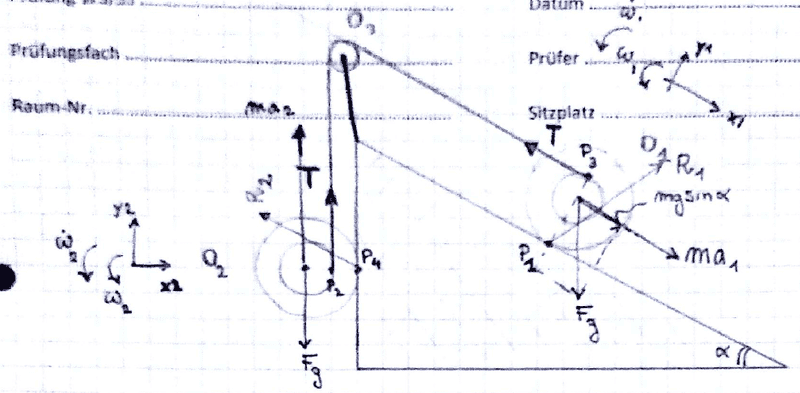
Starting from stillness @ t = 0, we are looking for the acceleration @T=0 of the 2 wheels (rolling without slip, in particular in point P4 we have a gear wheel contact so we can have that the reaction R2y of the plane could be also in direction y2, in this case, you can see that Reation R2x in direction x2 the reaction is 0).
The 2 wheels are connected with a not extendable Rope. Also Wheel 1 does not slip, so R1y = mgsin(alfa) with alfa = 30°, whereas R1x should be found.
the big radius of each wheel is R=20cm
The internal radius where the rope is rolled up is r = 10cm.
J of each wheel is 0.0125 kgm^2.
Weight of each wheel m = 1kg

Homework Equations

domega1 = - a_o1 / R ; % Angle acceleration wheel 1 ( positive domega1 in clockwise direction)
domega2 = - a_o2 / R ; % Angle acceleration wheel 2 (positive domega2 in clockwise direction)
eq1 (Forces equilibrium direction x1) : m * g* sin(alfa) - T + R1x = m * a_o1 ;
eq2 (Momentum equilibrium around P1): ( J + m * R^2) * domega1 = T * (R+r) - m * g *sin(alfa) * R - m * a_o1 * R ;
eq3 (Forces equilibrium direction y2): - m * g + T + R2y = m * a_o2 ;
eq4 (Momentum equilibrium around P4) : ( J + m * R^2) * domega2 = m * g * R - m * a_o2 * R - T * (R-r) ;
eq5 (cynematic relationship) : domega2 * (R-r) = domega1 * (R+r) ;

The Attempt at a Solution

Looking for:
a_01
a_02
T
R2y
R1x

I solve it with Matlab and i got a_02 about -23 m/s^2 which is in my opinion not acceptable.
What do i do wrong?

Thanks in advance!

 

[TSny]

Welcome to PF!

eq2 (Momentum equilibrium around P1): ( J + m * R^2) * domega1 = T * (R+r) - m * g *sin(alfa) * R - m * a_o1 * R

Can you explain why you included the last term on the right side?

domega1 = - a_o1 / R ; % Angle acceleration wheel 1 ( positive domega1 in clockwise direction)
domega2 = - a_o2 / R ; % Angle acceleration wheel 2 (positive domega2 in clockwise direction)

Did you mean to say counterclockwise here? Your diagram indicates that positive direction of rotation for both wheels is counterclockwise.

 

[parmalesso]

Welcome to PF!

"Can you explain why you included the last term on the right side?"

Because i am a idiot! As i saw now, I wrote erroneusly and to some extends accidentally into both Momentum Equilibrium equations the "resulting forces", i will correct the equation s and come back to you.

Did you mean to say counterclockwise here? Your diagram indicates that positive direction of rotation for both wheels is counterclockwise.

YES I meant counterclockwise, the equations are positive in the counterclowise , i.e. coherent with the diagramm.

 

[parmalesso]

I solved it. I rewrote the equations:

domega1 = - a_o1 / R ; % Angle acceleration wheel 1 (positive domega1 in counterclockwise direction)
domega2 = - a_o2 / R ; % Angle acceleration wheel 2 (positive domega2 in counterclockwise direction)

Equilibrium of the Forces for wheel 1 along x1
m * g* sin(alfa) - T + R1x = m * a_o1 ;
Equilibrium of the Moments for wheel 1 around P1
( J + m * R^2) * domega1 = T * (R+r) - m * g *sin(alfa) * R ;
Equilibrium of the Forces for wheel 2 along y2
- m * g + T + R2y = m * a_o2 ;
Equilibrium of the Moments for wheel 2 around P4
( J + m * R^2) * domega2 = m * g * R - T * (R-r) ;
Cinematic Relationship
domega2 * (R-r) = domega1 * (R+r) ;

And I obtain:
R and J are given:
R = 2 * r;
J = 5/4 m r^2

therefore:
T = (g*m)/2
a_o1 = -(4*g)/21
a_o2 = -(4*g)/7
R1x = -(4*g*m)/21
R2y = -(g*m)/14

 

[TSny]

That all looks good to me. Nice work.