Usage of General Specific Heats Cp0 and Cv0

[messier992]

Homework Statement

What conditions for usage of the general specific heats?

Relevant Equations

u2-u1=~Cv0(T2-T1)
h2-h1=~Cp0(T2-T1)
Cv=du/DT at constant volume
Cp=dh/dT at constant Pressure
Q-W=me*he-mi*hi+m2*u

1. I am rather confused about the usage of Cp0 and Cv0 in the solutions to the question below:

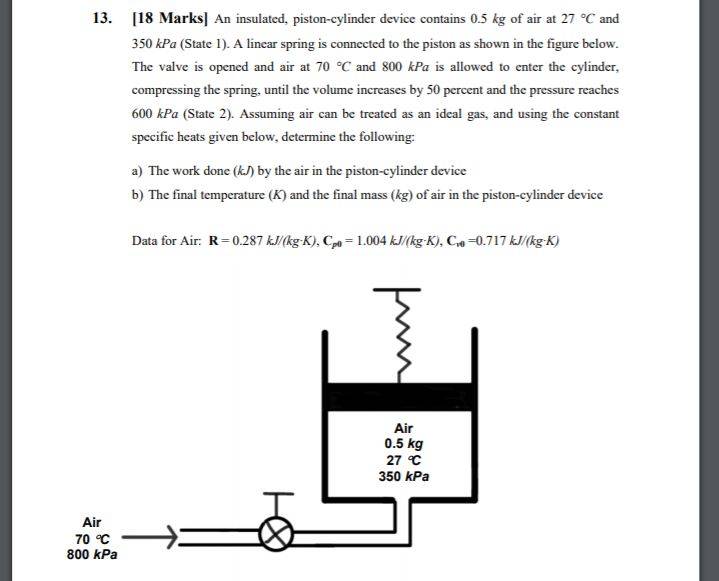
In the solution to the depicted question, the solution involves setting up the equation as follows:
Q-W=m_e*h_e-m_i*h_i+m₂*u_e-m₁*u₁
-W=-m_i*Cp*T_i+m₂CvT₂-m₁CvT₁
I don't follow for the second step. How can the transformation of hi, u1, and u2 be valid? I thought the relation between Cp0 and Cv0 only held over an interval due to the nature of the derivation of the equations:
Cv=δu/δT at constant volume => ∫Cvδu=∫δT => u2-u1=~Cv0(T2-T1)
Cp=δh/δT at constant Pressure = ∫Cvδu=∫δT => h2-h1=~Cp0(T2-T1)2. Additionally, what are the conditions for the usage of these equations?
u2-u1=~Cv0(T2-T1)
h2-h1=~Cp0(T2-T1)
I thought they were only valid at constant volume and pressure? In the case above, the pressure/volume changes linearly, are the relations still valid then?
Lastly, mass is also added between states 1 and 2, in the case above. I understand the equation relates specific terms, per unit mass, but does this addition of mass pose a problem?

 

[Chestermiller]

1. I am rather confused about the usage of Cp0 and Cv0 in the solutions to the question below:
View attachment 242473
In the solution to the depicted question, the solution involves setting up the equation as follows:
Q-W=m_e*h_e-m_i*h_i+m₂*u_e-m₁*u₁
-W=-m_i*Cp*T_i+m₂CvT₂-m₁CvT₁
I don't follow for the second step. How can the transformation of hi, u1, and u2 be valid? I thought the relation between Cp0 and Cv0 only held over an interval due to the nature of the derivation of the equations:
Cv=δu/δT at constant volume => ∫Cvδu=∫δT => u2-u1=~Cv0(T2-T1)
Cp=δh/δT at constant Pressure = ∫Cvδu=∫δT => h2-h1=~Cp0(T2-T1)

The assumption is made that, over the temperature range of interest, the heat capacities are constant. If the answer had employed a reference temperature other than absolute zero (say, 27 C, for example), the 2nd equation would have come out the same in the end, but the derivation would have been much more acceptable to you

2. Additionally, what are the conditions for the usage of these equations?
u2-u1=~Cv0(T2-T1)
h2-h1=~Cp0(T2-T1)
I thought they were only valid at constant volume and pressure? In the case above, the pressure/volume changes linearly, are the relations still valid then?

For the special case of an ideal gas, the thermodynamic state functions u and h are functions only of temperature, independent of pressure and volume, so it doesn't matter if the pressure and volume changed.

Lastly, mass is also added between states 1 and 2, in the case above. I understand the equation relates specific terms, per unit mass, but does this addition of mass pose a problem?

Well, you need to determine the change in mass $m_i=m_2-m_1$, so you would write $$m_2=m_1+m_i$$

 

[messier992]

Thanks for the reply! I am still confused about how hi can transform into Cp*Ti. I know there is a relationship between Δh = Cp(ΔT), but do not know if there is one for h=CpT. Or are there more complicated immediate steps in between the aforementioned Steps 1 & 2 that were not in the solution?

 

[Chestermiller]

Thanks for the reply! I am still confused about how hi can transform into Cp*Ti. I know there is a relationship between Δh = Cp(ΔT), but do not know if there is one for h=CpT. Or are there more complicated immediate steps in between the aforementioned Steps 1 & 2 that were not in the solution?

If we let $T_R$ represent some arbitrary datum absolute temperature at which the internal energy per unit mass is $u_R$, then in the open system (control volume) version of the 1 st law applied to this problem, then we would write $$u=u_R+C_{v0}(T-T_R)$$ and $$h=u+Pv=u+RT=u_R+C_{v0}(T-T_R)+RT=C_{p0}(T-T_R)+u_R+RT_R$$The energy balance would be written as:$$m_2u_2-m_1u_1=m_ih_i+Q-W$$If we then substitute the equations for u and h in terms of the reference temperature $T_R$, we obtain:$$m_2C_{v0}T_2-m_1C_{v0}T_1+(m_2-m_1)(u_R-C_{v0}T_R)=m_iC_{p0}T_i+m_i(u_R-C_{p0}T_R+RT_R)+Q-W$$But, since $m_2-m_1=m_i$, the terms involving the reference state temperature $T_R$ and reference state internal energy $u_R$ drop out, and we are left with:$$m_2C_{v0}T_2-m_1C_{v0}T_1=m_iC_{p0}T_i+Q-W$$