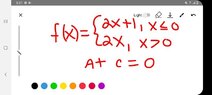nycmathguy
- Homework Statement
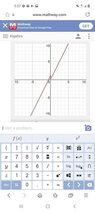
- Use the graph of f(x) to investigate the limit.
- Relevant Equations
- Piecewise-defined Function
Use the graph to investigate the limit of f(x) as x tends to c at the number c.
See attachments.
Based on the graph of f(x), here is what I did:
lim (2x + 1) as x tends to 0 from the left is 1.
lim (2x) as x tends to 0 from the right is 0.
LHL does not equal RHL.
I conclude the limit of f(x) as x tends to c at the number c (c = 0) does not exist.
See attachments.
Based on the graph of f(x), here is what I did:
lim (2x + 1) as x tends to 0 from the left is 1.
lim (2x) as x tends to 0 from the right is 0.
LHL does not equal RHL.
I conclude the limit of f(x) as x tends to c at the number c (c = 0) does not exist.